题目内容
11.已知a,b,c分别为△ABC三个内角A,B,C的对边,a=2,且有(2+b)(sinA-sinB)=(c-b)sinC.(Ⅰ)求角A的值;
(Ⅱ)求△ABC周长的取值范围.
.
分析 (Ⅰ)由条件利用正弦定理可得b2+c2-bc=4.再由余弦定理可得A的值.
(Ⅱ)利用正弦定理,三角形内角和定理,三角函数恒等变换的应用可得周长=$2+4sin(B+\frac{π}{6})$,由B的范围可求$\frac{π}{6}<B+\frac{π}{6}<\frac{5π}{6}$,利用正弦函数的图象和性质可求取值范围.
解答 解:(Ⅰ)(2+b)(sinA-sinB)=(c-b)sinC⇒(a+b)(a-b)=(c-b)c
化简得:b2+c2-a2=bc,
所以:$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{1}{2}$.
因为:A∈(0,π),
可得:A=$\frac{π}{3}$.
(Ⅱ)△ABC周长=a+b+c=2+2RsinB+2RsinC
=$2+\frac{a}{sinA}sinB+\frac{a}{sinB}sin(A+B)$=$2+\frac{{4\sqrt{3}}}{3}(sinB+sin({60°}+B))$
=$2+\frac{{4\sqrt{3}}}{3}(sinB+sin({60°}+B))$=$2+4sin(B+\frac{π}{6})$;
∵$0<B<\frac{2π}{3}$,
∴$\frac{π}{6}<B+\frac{π}{6}<\frac{5π}{6}$,$\frac{1}{2}<sin(B+\frac{π}{6})≤1$;
∴周长的取值范围是(4,6].
点评 本题主要考查了正弦定理,余弦定理,三角函数恒等变换的应用,正弦函数的图象和性质在解三角形中的应用,考查了转化思想,属于中档题.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
2.设a=log48,b=log0.48,c=20.4,则( )
| A. | b<c<a | B. | c<b<a | C. | c<a<b | D. | b<a<c |
 四棱锥P-ABCD中,点P在平面ABCD内的射影H在棱AD上,PA⊥PD,底面ABCD是梯形,BC∥AD,AB⊥AD,且AB=BC=1,AD=2.
四棱锥P-ABCD中,点P在平面ABCD内的射影H在棱AD上,PA⊥PD,底面ABCD是梯形,BC∥AD,AB⊥AD,且AB=BC=1,AD=2.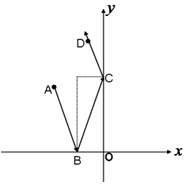 (1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;
(1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;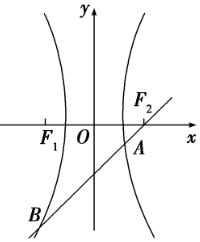 过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求:
过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求: