题目内容
15.函数f(x)=log${\;}_{\frac{1}{2}}$-x的零点在区间(n,n+1)(n∈N)内,则n=0.分析 易知函数f(x)=log${\;}_{\frac{1}{2}}$x-x在其定义域上连续单调递减,从而利用零点的判定定理解得.
解答 解:易知函数f(x)=log${\;}_{\frac{1}{2}}$x-x在其定义域上连续单调递减,
∵f($\frac{1}{2}$)=$\frac{1}{2}$>0,
f(1)=-1<0,
故函数f(x)=log${\;}_{\frac{1}{2}}$x-x的零点在区间(0,1)上,
故n=0,
故答案为:0.
点评 本题考查了函数的性质的判断与零点的判定定理的应用.

练习册系列答案
相关题目
5.已知等差数列{an}中,a1+a9=16,a4=1,则a13的值是( )
| A. | 15 | B. | 30 | C. | 31 | D. | 64 |
7. 学校小卖部货架上摆放着某品牌方便面,它们的三视图如图,则货架上的方便面至少有( )
学校小卖部货架上摆放着某品牌方便面,它们的三视图如图,则货架上的方便面至少有( )
 学校小卖部货架上摆放着某品牌方便面,它们的三视图如图,则货架上的方便面至少有( )
学校小卖部货架上摆放着某品牌方便面,它们的三视图如图,则货架上的方便面至少有( )| A. | 7盒 | B. | 8盒3 | C. | 9盒 | D. | 10盒 |
5.不等式x(3-x)≥0的解集是( )
| A. | {x|x≤0或x≥3} | B. | {x|0≤x≤3} | C. | {x|x≥3} | D. | {x|x≤3} |
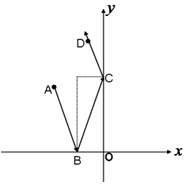 (1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;
(1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;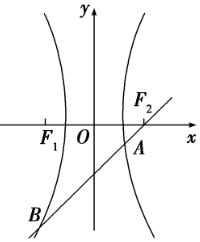 过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求:
过双曲线$\frac{{x}^{2}}{9}$-$\frac{{y}^{2}}{16}$=1的右焦点作倾斜角为45°的弦AB.求: