题目内容
14.在△ABC中,B=$\frac{π}{4}$,BC边上的高等于$\frac{1}{3}$BC,则cosA=-$\frac{\sqrt{10}}{10}$.分析 作出图形,令∠DAC=θ,依题意,可求得cosθ═$\frac{AD}{AC}$=$\frac{\frac{a}{3}}{\sqrt{(\frac{1}{3}a)^{2}+(\frac{2}{3}a)^{2}}}$=$\frac{\sqrt{5}}{5}$,sinθ=$\frac{2\sqrt{5}}{5}$,利用两角和的余弦即可求得答案.
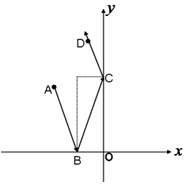
解答  解:设△ABC中角A、B、C、对应的边分别为a、b、c,AD⊥BC于D,令∠DAC=θ,
解:设△ABC中角A、B、C、对应的边分别为a、b、c,AD⊥BC于D,令∠DAC=θ,
∵在△ABC中,B=$\frac{π}{4}$,BC边上的高AD=h=$\frac{1}{3}$BC=$\frac{1}{3}$a,
∴BD=AD=$\frac{1}{3}$a,CD=$\frac{2}{3}$a,
在Rt△ADC中,cosθ=$\frac{AD}{AC}$=$\frac{\frac{a}{3}}{\sqrt{(\frac{1}{3}a)^{2}+(\frac{2}{3}a)^{2}}}$=$\frac{\sqrt{5}}{5}$,故sinθ=$\frac{2\sqrt{5}}{5}$,
∴cosA=cos($\frac{π}{4}$+θ)=cos$\frac{π}{4}$cosθ-sin$\frac{π}{4}$sinθ=$\frac{\sqrt{2}}{2}×\frac{\sqrt{5}}{5}$-$\frac{\sqrt{2}}{2}×\frac{2\sqrt{5}}{5}$=-$\frac{\sqrt{10}}{10}$.
故答案为:-$\frac{\sqrt{10}}{10}$.
点评 本题考查解三角形中,作出图形,令∠DAC=θ,利用两角和的余弦求cosA是关键,也是亮点,属于中档题.

练习册系列答案
相关题目
5.已知等差数列{an}中,a1+a9=16,a4=1,则a13的值是( )
| A. | 15 | B. | 30 | C. | 31 | D. | 64 |
2.设a=log48,b=log0.48,c=20.4,则( )
| A. | b<c<a | B. | c<b<a | C. | c<a<b | D. | b<a<c |
9.点P(tan 2015°,cos 2015°)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 (1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;
(1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;