题目内容
1.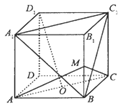 如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,M为棱BB1的中点,则下列结论中错误的是( )| A. | D1O∥平面A1BC1 | B. | D1O⊥平面MAC | ||
| C. | 异面直线BC1与AC所成的角为60° | D. | MO与底面所成角为90° |
分析 由线面平行的判定证明A正确;由线面垂直的判定说明B正确;由异面直线所成角的概念结合正方体的面对角线相等说明C正确;求出∠MOB为二面角M-AC-B的平面角,从而得到D错误.
解答 解:如图, 连接B1D1,交A1C1于N,则可证明OD1∥BN,
连接B1D1,交A1C1于N,则可证明OD1∥BN,
由OD1?面A1BC1,BN?面A1BC1,可得D1O∥面A1BC1,A正确;
由三垂线定理的逆定理可得OD1⊥AC,
设正方体棱长为2,可求得OM2=3,OD12=6,MD12=9,
则OD12+OM2=D1M2,有OD1⊥OM,由线面垂直的判定可得D1O⊥平面AMC,
B正确;
由正方体的面对角线相等得到△A1BC1为正三角形,即∠A1C1B=60°,
∴异面直线BC1与AC所成的角等于60°,C正确;
因为BO⊥AC,MO⊥AC,∴∠MOB为二面角M-AC-B的平面角,
显然MO与底面所成的角不是90°,故D不正确;
故选:D.
点评 本题考查了空间直线和平面的位置关系,考查了异面直线所成角的求法,训练了利用等积法求点到面的距离,是中档题.

练习册系列答案
相关题目
12.已知复数z满足(2-i)z=5,则z=( )
| A. | 2+i | B. | 2-i | C. | -2-i | D. | -2+i |
9.点P(tan 2015°,cos 2015°)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
16.已知函数f(x)=$\left\{\begin{array}{l}{lgx,x>0}\\{{3}^{x-1},x≤0}\end{array}\right.$,则f(f(1))=( )
| A. | $\frac{1}{3}$ | B. | 3 | C. | 1 | D. | $\frac{1}{9}$ |
13.下列函数中,既是奇函数又增函数的为( )
| A. | y=x+1 | B. | y=-x2 | C. | y=-$\frac{1}{x}$ | D. | y=x|x| |
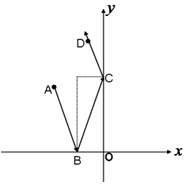 (1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;
(1)已知A(-2,-3),B(3,0),直线l过点P(-1,2),且与线段AB相交,求直线l的斜率K的取值范围;