题目内容
15.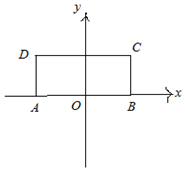 如图,在矩形ABCD中,AB=12,BC=5,以A、B为焦点的双曲线$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$恰好过C、D两点,则双曲线M的标准方程为$\frac{x^2}{16}-\frac{y^2}{20}=1$.
如图,在矩形ABCD中,AB=12,BC=5,以A、B为焦点的双曲线$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$恰好过C、D两点,则双曲线M的标准方程为$\frac{x^2}{16}-\frac{y^2}{20}=1$.
分析 根据题意,求出A、B、C、D四点的坐标,分析可得c=6,由双曲线的定义可得2a=||AC|-|CB||=13-5=8,即a=4,由双曲线的性质可得b的值,将a、b的值代入双曲线方程即可得答案.
解答 解:根据题意,分析可得A:(-6,0),B(6,0),D(-6,5),C(6,5),则|AC|=$\sqrt{1{2}^{2}+{5}^{2}}$=13,
若双曲线的焦点为A、B,则c=6,
又由双曲线恰好过C、D两点,则2a=||AC|-|CB||=13-5=8,即a=4,
又由c=6,则b2=a2-c2=20;
则双曲线的方程为:$\frac{x^2}{16}-\frac{y^2}{20}=1$;
故答案为:$\frac{x^2}{16}-\frac{y^2}{20}=1$.
点评 本题考查双曲线的几何性质,关键是掌握双曲线的定义,分析得到a、c的值.

练习册系列答案
相关题目
5.下列说法中正确的是( )
| A. | 一个命题的逆命题为真,则它的逆否命题一定为真 | |
| B. | 若“ac2>bc2”,则a>b | |
| C. | ?x0∈R,$sin{x_0}+cos{x_0}=\frac{3}{2}$ | |
| D. | “a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0” |
6.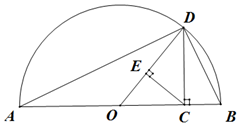 若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
 若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )
若a>0,b>0,则称$\frac{2ab}{a+b}$为a,b的调和平均数.如图,点C为线段AB上的点,且AC=a,BC=b,点O为线段AB中点,以AB为直径做半圆,过点C作AB的垂线交半圆于D,连结OD,AD,BD.过点C作OD的垂线,垂足为E,则图中线段OD的长度是a,b的算术平均数,那么图中表示a,b的几何平均数与调和平均数的线段,以及由此得到的不等关系分别是( )| A. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | B. | $CD,DE,\frac{2ab}{a+b}≤\sqrt{ab}$ | C. | $CD,CE,\frac{2ab}{a+b}≥\sqrt{ab}$ | D. | $CD,CE,\frac{2ab}{a+b}≤\sqrt{ab}$ |
3.下列说法正确的是( )
| A. | 命题“若x2=9,则x=±3”的否命题为“若x2=9,则x≠±3” | |
| B. | 若命题P:?x0∈R,$x_0^2-3{x_0}-1>0$,则命题?P:?x∈R,$x_{\;}^2-3x-1<0$ | |
| C. | 设$\overrightarrow a,\overrightarrow b$是两个非零向量,则“$\overrightarrow a•\overrightarrow b<0$是“$\overrightarrow a,\overrightarrow b$夹角为钝角”的必要不充分条件 | |
| D. | 若命题P:$\frac{1}{x-2}>0$,则¬P:$\frac{1}{x-2}≤0$ |
5.在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,AB=2BC,E是CD上一点,若AE⊥平面PBD,则$\frac{CE}{ED}$的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
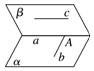 如图,已知平面α∩平面β=直线a,直线b?α,直线c?β,b∩a=A,c∥a.求证:b与c是异面直线.
如图,已知平面α∩平面β=直线a,直线b?α,直线c?β,b∩a=A,c∥a.求证:b与c是异面直线.