题目内容
5.在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,AB=2BC,E是CD上一点,若AE⊥平面PBD,则$\frac{CE}{ED}$的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 3 | D. | 4 |
分析 推导出PD⊥AE,当AE⊥BD时,AE⊥平面PBD,此时△ABD∽△DAE,由此能求出$\frac{CE}{ED}$的值.
解答  解:∵PD⊥底面ABCD,∴PD⊥AE,
解:∵PD⊥底面ABCD,∴PD⊥AE,
当AE⊥BD时,AE⊥平面PBD,此时△ABD∽△DAE,
则$\frac{AB}{AD}=\frac{AD}{DE}$,
∵AB=2BC,∴DE=$\frac{1}{4}AB$=$\frac{1}{4}$CD,
∴$\frac{CE}{ED}$=3.
故选:C.
点评 本题考查两线段长的比值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力、空间想象能力,考查化归与转化思想、数形结合思想、函数与方程思想,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.若定义在R上的函数f(x)满足:(Ⅰ)f(x1+x2)=f(x1)•f(x2),(Ⅱ)?x1<x2,f(x1)>f(x2),则满足以上条件的一个函数解析式为y=($\frac{1}{3}$)x.
10.设命题p:?x0∈(0,+∞),lnx0=-1.命题q:若m>1,则椭圆$\frac{{x}^{2}}{m}$+y2=1的焦距为2$\sqrt{m-1}$,那么,下列命题为真命题的是( )
| A. | ¬q | B. | (¬p)∨(¬q) | C. | p∧q | D. | p∧(¬q) |
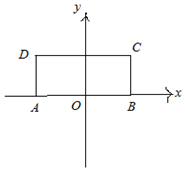 如图,在矩形ABCD中,AB=12,BC=5,以A、B为焦点的双曲线$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$恰好过C、D两点,则双曲线M的标准方程为$\frac{x^2}{16}-\frac{y^2}{20}=1$.
如图,在矩形ABCD中,AB=12,BC=5,以A、B为焦点的双曲线$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$恰好过C、D两点,则双曲线M的标准方程为$\frac{x^2}{16}-\frac{y^2}{20}=1$.