题目内容
10．
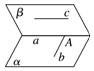如图，已知平面α∩平面β=直线a，直线b?α，直线c?β，b∩a=A，c∥a．求证：b与c是异面直线．
分析 假设b与c共面，设b与c确定的平面为γ，推导出a∥γ，从而a∥b，与a∩b=A矛盾，由此能证明b与c是异面直线．
解答 证明：（利用反证法）
假设b，c不是异面直线，即b与c共面，设b与c确定的平面为γ，则γ∩α=b，γ∩β=c．
∵a∥c，a?γ，∴a∥γ．
又∵a?α，且α∩γ=b，∴a∥b，这与a∩b=A矛盾．
因此b与c不可能共面，故b与c是异面直线．
点评 本题考查两直线是异面直线的证明，考查反证法、异面直线等基础知识，考查数形结合思想，是基础题．
练习册系列答案
相关题目
5．已知离心率为e的双曲线$\frac{x^2}{a^2}-\frac{y^2}{7}=1$，其与椭圆$\frac{x^2}{25}+\frac{y^2}{9}=1$的焦点重合，则e的值为（ ）
| A． | $\frac{3}{4}$ | B． | $\frac{4\sqrt{23}}{23}$ | C． | $\frac{4}{3}$ | D． | $\frac{\sqrt{23}}{4}$ |
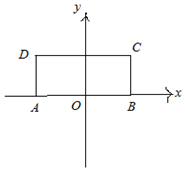如图，在矩形ABCD中，AB=12，BC=5，以A、B为焦点的双曲线$M：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$恰好过C、D两点，则双曲线M的标准方程为$\frac{x^2}{16}-\frac{y^2}{20}=1$．
19．设集合A={x|-1≤x＜1}，B={x|0＜x≤2}则集合A∪B=（ ）
| A． | {x|0＜x＜1} | B． | {x|-1≤x≤2} | C． | {x|-1＜x＜2} | D． | {x|0≤x≤1} |