题目内容
7.已知函数f(x)=(sinx+cosx)2+cos2x.( I)求f(x)的最小正周期;
( II)求f(x)在区间$[0,\frac{π}{2}]$上的最大值和最小值及相应的x值.
分析 ( I)利用三角恒等变换化简f(x)的解析式,再利用正弦函数的周期性求得f(x)的最小正周期.
( II)利用正弦函数的定义域和值域,求得f(x)在区间$[0,\frac{π}{2}]$上的最大值和最小值及相应的x值.
解答 解:( I)∵$f(x)={(sinx+cosx)^2}+cos2x=1+sin2x+cos2x=1+\sqrt{2}sin(2x+\frac{π}{4})$,
∴f(x)的最小正周期是π.
( II)∵$x∈[0,\frac{π}{2}]$,∴$2x+\frac{π}{4}∈[\frac{π}{4},\frac{5π}{4}]$,又 f(x)=1+$\sqrt{2}$sin(2x+$\frac{π}{4}$),
∴当$2x+\frac{π}{4}=\frac{π}{2}$,即$x=\frac{π}{8}$时,$f{(x)_{max}}=1+\sqrt{2}$;
当2x+$\frac{π}{4}$=$\frac{5π}{4}$时,即x=$\frac{π}{2}$时,f(x)取得最小值为1+$\sqrt{2}$•(-$\frac{\sqrt{2}}{2}$)=1-1=0.
点评 本题主要考查三角恒等变换,正弦函数的周期性,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
12.设x,y满足约束条件$\left\{\begin{array}{l}{3x-y-6≤0}\\{x-y+2≥0}\\{x≥0,y≥0}\end{array}\right.$若目标函数z=ax+by(a>0,b>0)的值是最大值为12,则$\frac{2b+3a}{ab}$的最小值为( )
| A. | $\frac{25}{6}$ | B. | $\frac{8}{3}$ | C. | $\frac{11}{3}$ | D. | 4 |
19.设集合A={x|-1≤x<1},B={x|0<x≤2}则集合A∪B=( )
| A. | {x|0<x<1} | B. | {x|-1≤x≤2} | C. | {x|-1<x<2} | D. | {x|0≤x≤1} |
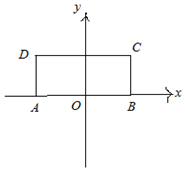 如图,在矩形ABCD中,AB=12,BC=5,以A、B为焦点的双曲线$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$恰好过C、D两点,则双曲线M的标准方程为$\frac{x^2}{16}-\frac{y^2}{20}=1$.
如图,在矩形ABCD中,AB=12,BC=5,以A、B为焦点的双曲线$M:\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$恰好过C、D两点,则双曲线M的标准方程为$\frac{x^2}{16}-\frac{y^2}{20}=1$.