题目内容
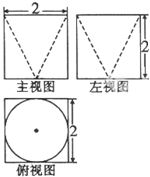
某几何体的三视图如图所示，则它的表面积是（ ）
A、24+
| ||
| B、24-π | ||
C、24+(
| ||
D、20+(
|
考点：由三视图求面积、体积
专题：计算题,空间位置关系与距离
分析：几何体为正方体挖去一个圆锥，根据三视图判断正方体的边长及挖去的圆锥的高和底面直径，求得母线长，根据几何体的表面积为正方体的表面积加圆锥的侧面积，再减去圆锥的底面面积，把数据代入公式计算．
解答：
解：由三视图知：几何体为正方体挖去一个圆锥，且正方体的边长为2，
挖去的圆锥的高为2，底面直径为2，∴母线长为
，
几何体的表面积为正方体的表面积加圆锥的侧面积，再减去圆锥的底面面积，
∴S=6×22+π×1×
-π×12=24+（
-1）π．
故选：C．
挖去的圆锥的高为2，底面直径为2，∴母线长为
| 5 |
几何体的表面积为正方体的表面积加圆锥的侧面积，再减去圆锥的底面面积，
∴S=6×22+π×1×
| 5 |
| 5 |
故选：C．
点评：本题考查了由三视图求几何体的表面积，根据三视图判断几何体的形状及数据所对应的几何量是关键．
练习册系列答案
相关题目
点A（2a，a-1）在以点C（0，1）为圆心，
为半径的圆上，则a的值为（ ）
| 5 |
| A、±1 | ||
| B、0或1 | ||
C、-1或
| ||
D、1或-
|
平面内点P（x，y）的坐标满足方程
=
，则动点P的轨迹是（ ）
| (x-1)2+(y-1)2 |
| |x+y-2| | ||
|
| A、椭圆 | B、双曲线 |
| C、抛物线 | D、直线 |
若集合M={x|y=
}，N={x|y=
}，则M∩N=（ ）
| x2-x3 |
2-(
|
| A、[-1，1] |
| B、[0，1] |
| C、（-∞，0]∪（[1，+∞） |
| D、（-∞，-1]∪[1，+∞） |
方程ax2+by2=1表示双曲线的必要不充分条件是（ ）
| A、a＜0且b＞0 |
| B、a＞0且b＜0 |
| C、ab＜5 |
| D、ab＞0 |
若复数z满足（-1+i）z=2，则下面四个命题中真命题的为（ ）
p1：|z|=2
p2：z2是纯虚数
p3：z的共轭复数为1+i
p4：z的虚部为-1．
p1：|z|=2
p2：z2是纯虚数
p3：z的共轭复数为1+i
p4：z的虚部为-1．
| A、p1，p2 |
| B、p2，p3 |
| C、p3，p4 |
| D、p2，p4 |