题目内容
给定下列四个命题：
①若一条直线与一个平面平行，那么这条直线平行于这个平面内的任一直线；
②若一条直线与一个平面垂直，那么这条直线垂直于这个平面内的任一直线；
③若两个平面平行，那么分别在两个平面内的直线平行；
④若两个平面垂直，那么一个平面内垂直于交线的直线与另一个平面垂直．
其中，为真命题的是（ ）
①若一条直线与一个平面平行，那么这条直线平行于这个平面内的任一直线；
②若一条直线与一个平面垂直，那么这条直线垂直于这个平面内的任一直线；
③若两个平面平行，那么分别在两个平面内的直线平行；
④若两个平面垂直，那么一个平面内垂直于交线的直线与另一个平面垂直．
其中，为真命题的是（ ）
| A、①和② | B、②和③ |
| C、③和④ | D、②和④ |
考点：空间中直线与平面之间的位置关系
专题：开放型,空间位置关系与距离
分析：根据直线与平面、平面与平面之间的位置关系，依次分析命题，即可得出结论．
解答：
解：①若直线l平行平面α，则l与平面α内的任一条直线有两种位置关系：平行、异面，故①错误；
②如果一条直线垂直于一个平面，那么由直线与平面垂直的性质知：这条直线与这个平面内的任何直线垂直．故②正确；
③若两个平面平行，那么分别在两个平面内的直线平行、异面，故③错误；
④由面面垂直的性质定理知，两个平面垂直，那么一个平面内垂直于交线的直线与另一个平面垂直，正确．
故选：D．
②如果一条直线垂直于一个平面，那么由直线与平面垂直的性质知：这条直线与这个平面内的任何直线垂直．故②正确；
③若两个平面平行，那么分别在两个平面内的直线平行、异面，故③错误；
④由面面垂直的性质定理知，两个平面垂直，那么一个平面内垂直于交线的直线与另一个平面垂直，正确．
故选：D．
点评：本题主要考查了空间中直线与平面之间的位置关系，考查空间想象能力和思维能力．
练习册系列答案
名校课堂系列答案
相关题目
已知集合A={1，2，3，4}，B={2，4，6}，则A∩B的元素个数是（ ）
| A、0个 | B、1个 | C、2个 | D、3个 |
若抛物线C：y2=2px（p＞0）上一点到焦点和x轴的距离分别为5和3，则此抛物线的方程为（ ）
| A、y2=2x | ||
B、y2=（
| ||
| C、y2=2x或y2=18x | ||
D、y2=3x或y2=（
|
已知sinα+cosα=
，则sin2（
-α）=（ ）
| 1 |
| 3 |
| π |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
设0＜a＜b，且f（x）=
，则下列大小关系式成立的是（ ）
1+
| ||
| x |
A、f （a）＜f （
| ||||
B、f （
| ||||
C、f （
| ||||
D、f （b）＜f （
|
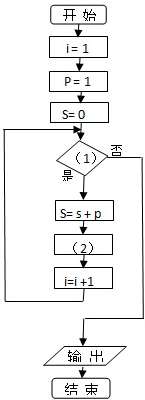给出50个数，1，2，4，7，11，…，其规律是：第1个数是1，第2个数比第1个数大1，第3个数比第2个数大2，第4个数比第3个数大3，…，以此类推．要求计算这50个数的和．先将右面给出的程序框图补充完整，再将与其功能相当的程序语言补充完整，把答案写在下面空格上．