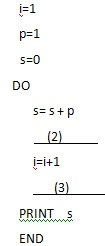题目内容
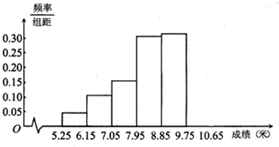 把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.25),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65),并绘制出频率分布直方图,如图所示的是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04、0.10、0.14、0.28、0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格.
把参加某次铅球投掷的同学的成绩(单位:米)进行整理,分成以下6个小组:[5.25,6.25),[6.15,7.05),[7.05,7.95),[7.95,8.85),[8.85,9.75),[9.75,10.65),并绘制出频率分布直方图,如图所示的是这个频率分布直方图的一部分.已知从左到右前5个小组的频率分别为0.04、0.10、0.14、0.28、0.30,第6小组的频数是7.规定:投掷成绩不小于7.95米的为合格.(Ⅰ)求这次铅球测试成绩合格的人数;
(Ⅱ)你认为这次铅球投掷的同学的成绩的中位数在第几组?请说明理由;
(Ⅲ)若参加这次铅球投掷的学生中,有5人的成绩为优秀,现在要从成绩优秀的学生中,随机选出2人参加相关部门组织的经验交流会,已知a,b两位同学的成绩均为优秀,求a,b两位同学中至少有1人被选到的概率.
考点:古典概型及其概率计算公式,频率分布直方图,众数、中位数、平均数
专题:概率与统计
分析:(Ⅰ)先求第6组的频率,从而确定这次铅球测试成绩合格的人数;
(Ⅱ)计算出第1、2、3组的人数为14人,第5、6组的人数为22人,所以可以确定这次铅球投掷的成绩的中位数在[7.95,8.85)内,即第4组;
(Ⅲ)列举随机选出2人参加相关部门组织的经验交流会的所有基本事件,找出a,b两位同学中至少有1人被选到所包含的基本事件,利用概率公式计算即可.
(Ⅱ)计算出第1、2、3组的人数为14人,第5、6组的人数为22人,所以可以确定这次铅球投掷的成绩的中位数在[7.95,8.85)内,即第4组;
(Ⅲ)列举随机选出2人参加相关部门组织的经验交流会的所有基本事件,找出a,b两位同学中至少有1人被选到所包含的基本事件,利用概率公式计算即可.
解答:
解:(Ⅰ)第6小组的频率为1-(0.04+0.10+0.28+0.30)=0.14,
∴参加这次铅球投掷的总人数为
=50人,
根据规定,第4、5、6组的成绩均为合格,
人数为(0.28+0.30+0.14)×50=36人;
(Ⅱ)∵成绩在第1、2、3组的人数为(0.04+0.10+0.14)×50=14人
成绩在第5、6组的人数为(0.30+0.14)×50=22人,
参加这次铅球投掷的总人数为50人,
∴这次铅球投掷的成绩的中位数在[7.95,8.85)内,即第4组;
(Ⅲ)设这次铅球投掷成绩优秀的5人为a、b、c、d、e,
则选出的2人所有可能的情况为:
ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10种,
其中a、b至少有1人的情况为:
ab,ac,ad,ae,bc,bd,be共7种,
∴a、b至少有1人被选到的概率为P=
.
∴参加这次铅球投掷的总人数为
| 7 |
| 0.14 |
根据规定,第4、5、6组的成绩均为合格,
人数为(0.28+0.30+0.14)×50=36人;
(Ⅱ)∵成绩在第1、2、3组的人数为(0.04+0.10+0.14)×50=14人
成绩在第5、6组的人数为(0.30+0.14)×50=22人,
参加这次铅球投掷的总人数为50人,
∴这次铅球投掷的成绩的中位数在[7.95,8.85)内,即第4组;
(Ⅲ)设这次铅球投掷成绩优秀的5人为a、b、c、d、e,
则选出的2人所有可能的情况为:
ab,ac,ad,ae,bc,bd,be,cd,ce,de,共10种,
其中a、b至少有1人的情况为:
ab,ac,ad,ae,bc,bd,be共7种,
∴a、b至少有1人被选到的概率为P=
| 7 |
| 10 |
点评:本题考查频率分布直方图的性质,样本数据的数字特征,古典概型概率的计算公式,列举法的应用,属于中档题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目
执行如图所示的程序框图.若输入的n的值为3,则输出的k的值为( )


| A、2 | B、3 | C、4 | D、5 |
若抛物线C:y2=2px(p>0)上一点到焦点和x轴的距离分别为5和3,则此抛物线的方程为( )
| A、y2=2x | ||
B、y2=(
| ||
| C、y2=2x或y2=18x | ||
D、y2=3x或y2=(
|
设0<a<b,且f(x)=
,则下列大小关系式成立的是( )
1+
| ||
| x |
A、f (a)<f (
| ||||
B、f (
| ||||
C、f (
| ||||
D、f (b)<f (
|
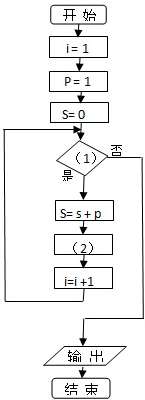 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.