题目内容
设函数f(x)=ax2+lnx.
(Ⅰ)当a=-1时,求函数y=f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)已知a<0,若函数y=f(x)的图象总在直线y=-
的下方,求a的取值范围.
(Ⅰ)当a=-1时,求函数y=f(x)的图象在点(1,f(1))处的切线方程;
(Ⅱ)已知a<0,若函数y=f(x)的图象总在直线y=-
| 1 |
| 2 |
考点:导数在最大值、最小值问题中的应用
专题:导数的综合应用
分析:(I)利用导数的几何意义可得切线的斜率,进而得到切线的方程;
(II)利用导数可得函数f(x)的极大值即可得到最大值,进而利用函数y=f(x)的图象总在直线y=-
的下方?f(x)max<-
即可解出.
(II)利用导数可得函数f(x)的极大值即可得到最大值,进而利用函数y=f(x)的图象总在直线y=-
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(Ⅰ)当a=-1时,由f(x)=-x2+lnx,
可得f/(x)=-2x+
,
∴f′(1)=-1,∴切线的斜率为-1.
又f(1)=-1,∴切点为(1,-1).
故所求的切线方程为:y+1=-(x-1),即x+y=0.
(Ⅱ)f′(x)=2ax+
=
=
,x>0,a<0.
令f′(x)=0,则x=
.
当x∈(0,
]时,f′(x)>0;当x∈(
,+∞)时,f′(x)<0.
故x=
为函数f(x)的唯一极大值点,
∴f(x)的最大值为f(
)=-
+
ln(-
).
由题意有-
+
ln(-
)<-
,解得a<-
.
∴a的取值范围为(-∞,-
).
可得f/(x)=-2x+
| 1 |
| x |
∴f′(1)=-1,∴切线的斜率为-1.
又f(1)=-1,∴切点为(1,-1).
故所求的切线方程为:y+1=-(x-1),即x+y=0.
(Ⅱ)f′(x)=2ax+
| 1 |
| x |
| 2ax2+1 |
| x |
2a(x2+
| ||
| x |
令f′(x)=0,则x=
-
|
当x∈(0,
-
|
-
|
故x=
-
|
∴f(x)的最大值为f(
-
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2a |
由题意有-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2a |
| 1 |
| 2 |
| 1 |
| 2 |
∴a的取值范围为(-∞,-
| 1 |
| 2 |
点评:本题考查了导数的几何意义、利用导数研究函数的单调性极值与最值、恒成立问题的等价转化问题等基础知识与基本技能方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
已知集合A={1,2,3,4},B={2,4,6},则A∩B的元素个数是( )
| A、0个 | B、1个 | C、2个 | D、3个 |
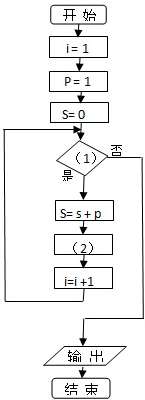 给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.
给出50个数,1,2,4,7,11,…,其规律是:第1个数是1,第2个数比第1个数大1,第3个数比第2个数大2,第4个数比第3个数大3,…,以此类推.要求计算这50个数的和.先将右面给出的程序框图补充完整,再将与其功能相当的程序语言补充完整,把答案写在下面空格上.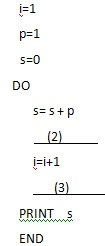
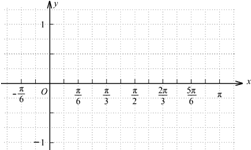 已知向量
已知向量