题目内容
设函数f(x)=a(x+1)2ln(x+1)+bx,曲线y=f(x)过点(e-1,e2-e+1),且在点(0,0)处的切线方程为y=0.
(1)求a,b的值;
(2)证明:当x≥0时,f(x)≥x2.
(1)求a,b的值;
(2)证明:当x≥0时,f(x)≥x2.
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由曲线y=f(x)过点(e-1,e2-e+1),代入可得ae2+b(e-1)=e2-e+1.f′(x)=2a(x+1)ln(x+1)+a(x+1)+b,由在点(0,0)处的切线方程为y=0.可得a+b=0,联立解出即可.
(2)由(1)可得:f(x)=(x+1)2ln(x+1)-x.当x≥0时,f(x)≥x2.即g(x)=(x+1)2ln(x+1)-x-x2≥0.x≥0.利用导数研究其单调性极值与最值即可.
(2)由(1)可得:f(x)=(x+1)2ln(x+1)-x.当x≥0时,f(x)≥x2.即g(x)=(x+1)2ln(x+1)-x-x2≥0.x≥0.利用导数研究其单调性极值与最值即可.
解答:
(1)解:∵曲线y=f(x)过点(e-1,e2-e+1),∴ae2+b(e-1)=e2-e+1.
f′(x)=2a(x+1)ln(x+1)+a(x+1)+b,
∵在点(0,0)处的切线方程为y=0.
∴a+b=0,
联立
,
解得a=1,b=-1.
(2)证明:由(1)可得:f(x)=(x+1)2ln(x+1)-x.当x≥0时,f(x)≥x2.即g(x)=(x+1)2ln(x+1)-x-x2≥0.x≥0.
g′(x)=2(x+1)(ln(x+1)-
),
当x>
-1时,g′(x)>0,此时函数g(x)单调递增;当0<x<
-1时,g′(x)>0,此时函数g(x)单调递减.
∴当x=
-1时,g(x)取得极小值即最小值,g(
-1)=
e-(
-1)-(e+1-2
)=
-
e>0,
∴g(x)>0,
∴当x≥0时,f(x)≥x2.
f′(x)=2a(x+1)ln(x+1)+a(x+1)+b,
∵在点(0,0)处的切线方程为y=0.
∴a+b=0,
联立
|
解得a=1,b=-1.
(2)证明:由(1)可得:f(x)=(x+1)2ln(x+1)-x.当x≥0时,f(x)≥x2.即g(x)=(x+1)2ln(x+1)-x-x2≥0.x≥0.
g′(x)=2(x+1)(ln(x+1)-
| 1 |
| 2 |
当x>
| e |
| e |
∴当x=
| e |
| e |
| 1 |
| 2 |
| e |
| e |
| e |
| 1 |
| 2 |
∴g(x)>0,
∴当x≥0时,f(x)≥x2.
点评:本题考查了利用导数研究其单调性极值与最值、导数几何意义、切线方程,考查了恒成立问题的等价转化方法,考查了推理能力与计算能力,属于难题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
| lim |
| △x→0 |
| f(x0+△x)-f(x0-△x) |
| 2△x |
A、
| ||
| B、f′(x0) | ||
| C、2f′(x0) | ||
| D、-f′(x0) |
 如图,△ABC内接于⊙O,点D在OC的延长线上,AD与⊙O相切,割线DM与⊙O相交于点M,N,若∠B=30°,AC=1,则DM×DN=
如图,△ABC内接于⊙O,点D在OC的延长线上,AD与⊙O相切,割线DM与⊙O相交于点M,N,若∠B=30°,AC=1,则DM×DN= 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2.
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2.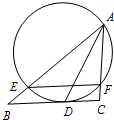 如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.
如图,过点A的圆与BC切于点D,且与AB、AC分别交于点E、F.已知AD为∠BAC的平分线,求证:EF∥BC.