题目内容
定义在R上的偶函数f(x),对任意实数x都有f(x+2)=f(x),当x∈[0,1]时,f(x)=x2,若在区间
[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是 .
[-1,3]内,函数g(x)=f(x)-kx-k有4个零点,则实数k的取值范围是
考点:函数零点的判定定理
专题:函数的性质及应用
分析:由题意可得,函数f(x)的图象和直线y=k(x+1)在区间[-1,3]内有4个交点,数形结合求得k的范围.
解答:
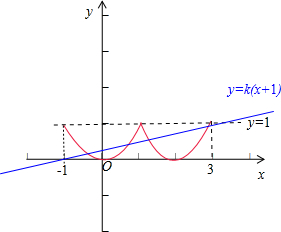 解:由题意可得,函数f(x)的周期为2,x∈[0,1]时,f(x)=x2,
解:由题意可得,函数f(x)的周期为2,x∈[0,1]时,f(x)=x2,
而f(x)是偶函数,
∴x∈[-1,1]时,f(x)=x2,
令y=kx+k,
在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点
即函数f(x)的图象和直线y=k(x+1)在区间[-1,3]内有4个交点,
如图所示:
故有 0<k(3+1)≤1,求得0<k≤
,
故答案为:(0,
].
 解:由题意可得,函数f(x)的周期为2,x∈[0,1]时,f(x)=x2,
解:由题意可得,函数f(x)的周期为2,x∈[0,1]时,f(x)=x2,而f(x)是偶函数,
∴x∈[-1,1]时,f(x)=x2,
令y=kx+k,
在区间[-1,3]内,函数g(x)=f(x)-kx-k有4个零点
即函数f(x)的图象和直线y=k(x+1)在区间[-1,3]内有4个交点,
如图所示:
故有 0<k(3+1)≤1,求得0<k≤
| 1 |
| 4 |
故答案为:(0,
| 1 |
| 4 |
点评:本题主要考查函数的零点与方程的根的关系,体现了转化、数形结合的数学思想,属于基础题.

练习册系列答案
相关题目
O为平行四边形ABCD所在平面上一点,若3|
|=2|
|,
+
=λ(
+
),
=μ(
+2
),则λ的值是( )
| AB |
| AD |
| OA |
| OB |
| OC |
| OD |
| OA |
| AB |
| AC |
A、-
| ||
B、-
| ||
C、-
| ||
| D、-1 |