题目内容
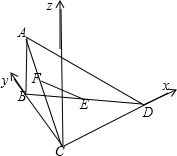
 如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2.
如图,在三棱锥A-BCD中,AB⊥平面BCD,BC⊥CD,∠CBD=60°,BC=2.(Ⅰ)求证:平面ABC⊥平面ACD;
(Ⅱ)若E是BD的中点,F为线段AC上的动点,EF与平面ABC所成的角记为θ,当tanθ的最大值为
| ||
| 2 |
考点:平面与平面垂直的判定,二面角的平面角及求法
专题:空间位置关系与距离,空间角
分析:(Ⅰ)直接根据已知条件,利用线线垂直,转化成线面垂直,最后转化出面面垂直.
(Ⅱ)首先建立空间直角坐标系,利用平面的法向量,建立等量关系,最后求出二面角平面角的余弦值.
(Ⅱ)首先建立空间直角坐标系,利用平面的法向量,建立等量关系,最后求出二面角平面角的余弦值.
解答:
 证明:(Ⅰ)在三棱锥A-BCD中,AB⊥平面BCD,
证明:(Ⅰ)在三棱锥A-BCD中,AB⊥平面BCD,
所以:AB⊥CD,
又∵BC⊥CD,
∴CD⊥平面ABC,
∵CD?平面ACD,
∴平面ABC⊥平面ACD.
(Ⅱ)建立空间直角坐标系C-xyz,
则:C(0,0,0),D(2
,0,0),B(0,2,0),E(
,1,0),
设A(0,2,t),
则:
=λ
=λ(0,2,t)
所以:F(0,2λ,tλ),
=(-
,2λ-1,tλ),
平面ABC的法向量为:
=(1,0,0),
由sinθ=
由于tanθ的最大值为
,
则:(t2+4)-4λ+4的最小值为
.
解得:t=4,
又∵BC⊥CD,AC⊥CD,
所以∠ACB就是二面角A-CD-B的平面角.
cos∠ACB=
=
.
 证明:(Ⅰ)在三棱锥A-BCD中,AB⊥平面BCD,
证明:(Ⅰ)在三棱锥A-BCD中,AB⊥平面BCD,所以:AB⊥CD,
又∵BC⊥CD,
∴CD⊥平面ABC,
∵CD?平面ACD,
∴平面ABC⊥平面ACD.
(Ⅱ)建立空间直角坐标系C-xyz,
则:C(0,0,0),D(2
| 3 |
| 3 |
设A(0,2,t),
则:
| CF |
| CA |
所以:F(0,2λ,tλ),
| EF |
| 3 |
平面ABC的法向量为:
| n |
由sinθ=
| 3 | ||
|
| ||
| 2 |
则:(t2+4)-4λ+4的最小值为
| 19 |
| 5 |
解得:t=4,
又∵BC⊥CD,AC⊥CD,
所以∠ACB就是二面角A-CD-B的平面角.
cos∠ACB=
| BC |
| AC |
| ||
| 5 |
点评:本题考查的知识要点:面面垂直的判定定理,二面角的应用,空间直角坐标系的应用,法向量的应用.及相关的运算问题.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
已知A(2,-4),B(0,6),C(-8,10),则
+2
为( )
| AB |
| BC |
| A、(18,18) |
| B、(-18,18) |
| C、(18,-18) |
| D、(-18,-18) |
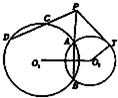 如图,⊙O1与⊙O2相交于A,B两点,点P在线段BA延长线上,T是⊙O1上一点,PT⊥O2T,过P的直线交⊙O1于C,D两点
如图,⊙O1与⊙O2相交于A,B两点,点P在线段BA延长线上,T是⊙O1上一点,PT⊥O2T,过P的直线交⊙O1于C,D两点