题目内容
已知函数y=
.
(1)求函数振幅、周期和频率;
(2)求函数的单调增区间和对称轴.
2sin(
| ||||
| 3 |
(1)求函数振幅、周期和频率;
(2)求函数的单调增区间和对称轴.
考点:正弦函数的图象,y=Asin(ωx+φ)中参数的物理意义
专题:三角函数的图像与性质
分析:(1)根据三角函数的解析式即可求函数振幅、周期和频率;
(2)结合三角函数的性质即可求函数的单调增区间和对称轴.
(2)结合三角函数的性质即可求函数的单调增区间和对称轴.
解答:
解:(1)y=
=
sin(
-
),
则函数振幅为
、周期T=
=4π,频率f=
=
;
(2)由2kπ-
≤
-
≤2kπ+
,k∈Z,
解得4kπ-
≤x≤4kπ+
,k∈Z,
故函数的单调增区间为[4kπ-
,4kπ+
],k∈Z,
由
-
=4kπ-
,解得x=4kπ-
,即函数的对称轴为x=4kπ-
,k∈Z.
2sin(
| ||||
| 3 |
| 2 |
| 3 |
| x |
| 2 |
| π |
| 4 |
则函数振幅为
| 2 |
| 3 |
| 2π | ||
|
| 1 |
| T |
| 1 |
| 4π |
(2)由2kπ-
| π |
| 2 |
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
解得4kπ-
| π |
| 2 |
| 3π |
| 2 |
故函数的单调增区间为[4kπ-
| π |
| 2 |
| 3π |
| 2 |
由
| x |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
点评:本题主要考查三角函数的图象和性质,要求熟练掌握三角函数的单调性,对称轴以及函数的周期等性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知平面向量
,
,|
|=2,
=(2,
),若|
-
|=
,则
•
的值是( )
| a |
| b |
| a |
| b |
| 3 |
| a |
| b |
| 6 |
| a |
| b |
A、
| ||
B、
| ||
C、
| ||
D、
|
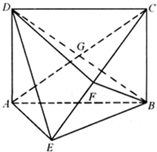 如图,矩形ABCD中.AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.
如图,矩形ABCD中.AD⊥平面ABE,BE=BC,F为CE上的点,且BF⊥平面ACE,G为AC与BD的交点.