题目内容
证明不等式：（a-c）2+4（a-b）（c-b）≥0．
考点：不等式的证明
专题：证明题,推理和证明
分析：展开合并，再配方，即可证明结论、
解答：
证明：（a-c）2+4（a-b）（c-b）=a2-2ac+c2+4ac-4ab-4bc+4b2
=a2+2ac+c2-4ab-4bc+4b2
=（a+c）2-4b（a+c）+4b2
=（a+c-2b）2≥0，
∴（a-c）2+4（a-b）（c-b）≥0．
=a2+2ac+c2-4ab-4bc+4b2
=（a+c）2-4b（a+c）+4b2
=（a+c-2b）2≥0，
∴（a-c）2+4（a-b）（c-b）≥0．
点评：本题考查不等式的证明，考查配方法的运用，比较简单．
练习册系列答案
相关题目
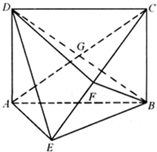如图，矩形ABCD中．AD⊥平面ABE，BE=BC，F为CE上的点，且BF⊥平面ACE，G为AC与BD的交点．已知A（2，-4），B（0，6），C（-8，10），则
+2
为（ ）
| AB |
| BC |
| A、（18，18） |
| B、（-18，18） |
| C、（18，-18） |
| D、（-18，-18） |