题目内容
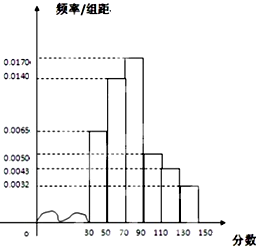 衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:
衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:(Ⅰ)求获得参赛资格的人数;
(Ⅱ)根据频率直方图,估算这500名学生测试的平均成绩;
(Ⅲ)若知识竞赛分初赛和复赛,在初赛中每人最多有5次选题答题的机会,累计答对3题或答错3题即终止,答对3题者方可参加复赛,已知参赛者甲答对每一个问题的概率都相同,并且相互之间没有影响,已知他连续两次答错的概率为
| 1 |
| 9 |
考点:离散型随机变量的期望与方差,频率分布直方图
专题:概率与统计
分析:(I)利用频率分布直方图能求出获得参赛资格的人数.
(II)利用频率分布直方图能求出这500名测试学生的平均成绩.
(III)由题设条件求出甲答对每一道题的概率
,ξ可能取得值为3,4,5,由此能求出ξ的分布列和数学期望.
(II)利用频率分布直方图能求出这500名测试学生的平均成绩.
(III)由题设条件求出甲答对每一道题的概率
| 2 |
| 3 |
解答:
解:(I)获得参赛资格的人数m=(0.005+0.0043+0.032)×20×500=125(2分)
(II)平均成绩:
=(40×0.0065+60×0.0140+80×0.0170+100×0.0050+120×0.0043+140×0.0032)×20
=(0.26+0.84+1.36+0.5+0.516+0.448)×20=78.48(5分)
(III)设甲答对每一道题的概率为.P
则(1-p)2=
,∴p=
,
∴ξ可能取得值为3,4,5,
P(ξ=3)=P3+(1-P)3=
,
P(ξ=4)=
P2(1-p)P+
(1-p)p(1-p)=
,
P(ξ=5)=1-
-
=
,
∴ξ的分布列为
Eξ=3×
+4×
+5×
=
.(12分)
(II)平均成绩:
. |
| X |
=(0.26+0.84+1.36+0.5+0.516+0.448)×20=78.48(5分)
(III)设甲答对每一道题的概率为.P
则(1-p)2=
| 1 |
| 9 |
| 2 |
| 3 |
∴ξ可能取得值为3,4,5,
P(ξ=3)=P3+(1-P)3=
| 1 |
| 3 |
P(ξ=4)=
| C | 2 3 |
| C | 2 3 |
| 10 |
| 27 |
P(ξ=5)=1-
| 1 |
| 3 |
| 10 |
| 27 |
| 8 |
| 27 |
∴ξ的分布列为
| ξ | 3 | 4 | 5 | ||||||
| P |
|
|
|
| 1 |
| 3 |
| 10 |
| 27 |
| 8 |
| 27 |
| 107 |
| 27 |
点评:本题考查频率直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题.

练习册系列答案
相关题目
设变量x,y满足约束条件
.目标函数z=x+2y,则z的取值范围为( )
|
| A、[1,2] |
| B、[1,11] |
| C、[2,11] |
| D、[0,11] |
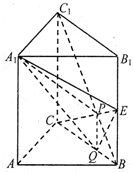 如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,E是BB1的中点,且CE交BC1于点P,点Q在线段BC上,CQ=2QB.
如图在直三棱柱ABC-A1B1C1中,∠BAC=90°,AB=AA1=2,E是BB1的中点,且CE交BC1于点P,点Q在线段BC上,CQ=2QB.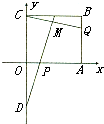 如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=
如图所示,在直角坐标平面上的矩形OABC中,|OA|=2,|OC|=