题目内容
在一次综合知识竞赛中,有两道填空题和两道解答题,填空题每题5分,解答题每题10分,某参赛者答对填空题的概率都是
,答对解答题的概率都是
,解答备题的结果是相互独立的.
(Ⅰ)求该参赛者恰好答对一道题的概率;
(Ⅱ)求该参赛者的总得分X的分布列及数学期望E(X).
| 3 |
| 4 |
| 2 |
| 3 |
(Ⅰ)求该参赛者恰好答对一道题的概率;
(Ⅱ)求该参赛者的总得分X的分布列及数学期望E(X).
考点:离散型随机变量的期望与方差,相互独立事件的概率乘法公式
专题:概率与统计
分析:(Ⅰ)设参赛者答对填空题为事件Ai(i=1,2),答对解答题为事件Bi(i=1,2),由此能求出该参赛者恰好答对一道题的概率.
(Ⅱ)由题意知X可能的取值为0,5,10,15,20,25,30,分别求出P(X=0),P(X=5),P(X=10),P(X=15),P(X=20),P(X=25),P(X=30),由此能求出X的分布列和EX.
(Ⅱ)由题意知X可能的取值为0,5,10,15,20,25,30,分别求出P(X=0),P(X=5),P(X=10),P(X=15),P(X=20),P(X=25),P(X=30),由此能求出X的分布列和EX.
解答:
解:(Ⅰ)设参赛者答对填空题为事件Ai(i=1,2),
答对解答题为事件Bi(i=1,2),
则有P(
B2)=P(
B1
)=(
)2×
×
=
,
P(A1
)=P(
A2
)=
×
×(
)2=
,
所以该参赛者恰好答对一道题的概率为:
P=2×
+2×
=
.
(Ⅱ)由题意知X可能的取值为0,5,10,15,20,25,30,
P(X=0)=P(
)=(
)2•(
)2=
,
P(X=5)=P(A1
)+P(
A2
)=2×
×
×(
)2=
,
P(X=10)=P(A1
)+P(
B2)+P(
B1
=(
)2×(
)2+2×(
)2×
×
=
,
P(X=15)=P(A1
B2)+P(A1
B1
)+P(
A2
B2)+P(
A2B1
)
=4×
×
×
×
=
.
P(X=20)=P(A1A2
B2)+P(A1A2B1
)+P(
B1B2)
=2×(
)2×
×
+(
)2×(
)2=
,
P(X=25)=P(
A2B1B2)+P(A1
B1B2)
=2×
×
×(
)2=
,
P(X=30)=P(A1A2B1B2)=(
)2(
)2=
,
∴X的分布列为:
∴EX=0×
+5×
+10×
+15×
+20×
+25×
+30×
=
.
答对解答题为事件Bi(i=1,2),
则有P(
. |
| A1 |
. |
| A2 |
. |
| B1 |
. |
| A1 |
. |
| A2 |
. |
| B2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 72 |
P(A1
. |
| A2 |
. |
| B1 |
. |
| B2 |
. |
| A1 |
. |
| B1 |
. |
| B2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 48 |
所以该参赛者恰好答对一道题的概率为:
P=2×
| 1 |
| 72 |
| 1 |
| 48 |
| 5 |
| 72 |
(Ⅱ)由题意知X可能的取值为0,5,10,15,20,25,30,
P(X=0)=P(
. |
| A1 |
. |
| A2 |
. |
| B1 |
. |
| B2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 144 |
P(X=5)=P(A1
. |
| A2 |
. |
| B1 |
. |
| B2 |
. |
| A1 |
. |
| B1 |
. |
| B2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 24 |
P(X=10)=P(A1
. |
| A2 |
. |
| B1 |
. |
| B2 |
. |
| A1 |
. |
| A2 |
. |
| B1 |
. |
| A1 |
. |
| A2 |
. |
| B2) |
=(
| 3 |
| 4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 13 |
| 144 |
P(X=15)=P(A1
. |
| A2 |
. |
| B1 |
. |
| A2 |
. |
| B2 |
. |
| A1 |
. |
| B1 |
. |
| A1 |
. |
| B2 |
=4×
| 1 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 6 |
P(X=20)=P(A1A2
. |
| B1 |
. |
| B2 |
. |
| A1 |
. |
| A2 |
=2×(
| 3 |
| 4 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 2 |
| 3 |
| 5 |
| 18 |
P(X=25)=P(
. |
| A1 |
. |
| A2 |
=2×
| 1 |
| 4 |
| 3 |
| 4 |
| 2 |
| 3 |
| 1 |
| 6 |
P(X=30)=P(A1A2B1B2)=(
| 2 |
| 4 |
| 2 |
| 3 |
| 1 |
| 4 |
∴X的分布列为:
| X | 0 | 5 | 10 | 15 | 20 | 25 | 30 | ||||||||||||||
| P |
|
|
|
|
|
|
|
| 1 |
| 144 |
| 1 |
| 24 |
| 13 |
| 144 |
| 1 |
| 6 |
| 5 |
| 18 |
| 1 |
| 6 |
| 1 |
| 4 |
| 125 |
| 6 |
点评:本题考查概率的求法,考查离散型随机事件的分布列和数学期望的求法,是中档题,在历年高考中都是必考题型.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
已知i是虚数单位,若复数z满足i=
,则z=( )
| 1-i |
| z |
| A、-1-i | B、-1+i |
| C、1-i | D、1+i |
设集合A={x|0<x≤3},B={x|x<-1,或x>2},则A∩B=( )
| A、(2,3] |
| B、(-∞,-1)∪(0,+∞) |
| C、(-1,3] |
| D、(-∞,0)∪(2,+∞) |
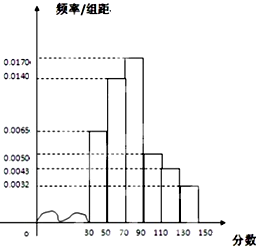 衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:
衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图: