题目内容
已知△ABC的三个内角A,B,C所对的边分别为a,b,c,且满足(b-a)(sinB+sinA)=(b-c)sinC,cosC=
,a=3.
(Ⅰ)求sinB;
(Ⅱ)求△ABC的面积.
| ||
| 3 |
(Ⅰ)求sinB;
(Ⅱ)求△ABC的面积.
考点:正弦定理,余弦定理
专题:三角函数的求值
分析:(Ⅰ)利用正弦定理化简已知等式得到关系式,再利用余弦定理表示出cosA,将得出的关系式代入求出cosA的值,确定出A的度数,由cosC的值求出sinC的值,将sinB变形为sin(A+C),利用两角和与差的正弦函数公式化简,把各自的值代入计算即可求出值;
(Ⅱ)由a,sinA,sinC的值,利用正弦定理求出c的值,利用三角形面积公式即可求出三角形ABC的面积.
(Ⅱ)由a,sinA,sinC的值,利用正弦定理求出c的值,利用三角形面积公式即可求出三角形ABC的面积.
解答:
解:(Ⅰ)由正弦定理化简已知等式得:(b-a)(b+a)=c(b-c),
即b2+c2-a2=bc,
∴cosA=
=
,
∵A为三角形的内角,
∴A=
,
∵cosC=
,
∴sinC=
=
,
∴sinB=sin(A+C)=sinAcosC+cosAsinC=
×
+
×
=
;
(Ⅱ)在△ABC中,由正弦定理
=
,得:
=
,即c=2
,
则S△ABC=
acsinB=
×3×2
×
=
.
即b2+c2-a2=bc,
∴cosA=
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
∵A为三角形的内角,
∴A=
| π |
| 3 |
∵cosC=
| ||
| 3 |
∴sinC=
| 1-cos2C |
| ||
| 3 |
∴sinB=sin(A+C)=sinAcosC+cosAsinC=
| ||
| 2 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 3 |
3+
| ||
| 6 |
(Ⅱ)在△ABC中,由正弦定理
| a |
| sinA |
| c |
| sinC |
| 3 | ||||
|
| c | ||||
|
| 2 |
则S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
3+
| ||
| 6 |
3
| ||||
| 2 |
点评:此题考查了正弦、余弦定理,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知全集U=R,集合A={x|x2-9≤0},B={x|log2x>0},则A∩∁UB=( )
| A、{x|0x<3} |
| B、{x|-3≤x≤1} |
| C、{x|x<0} |
| D、{x|1<x≤3} |
设min{f(x),g(x)}=
.若f(x)=x2+px+q的图象经过两点(α,0),(β,0),且存在整数n,使得n<α<β<n+1成立,则( )
|
A、min{f(n),f(n+1)}>
| ||
B、min{f(n),f(n+1)}<
| ||
C、min{f(n),f(n+1)}=
| ||
D、min{f(n),f(n+1)}≥
|
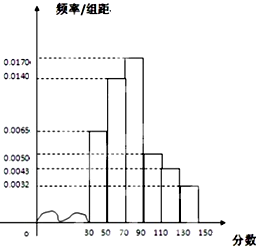 衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:
衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图: