题目内容
已知△ABC中,角A,B,C的对边分别为a,b,c,若向量
=(cosB,2cos2
-1)与向量
=(2a-b,c)共线.
(1)求角C的大小;
(2)若c=2
,S△ABC=2
,求a,b的值.
| m |
| C |
| 2 |
| n |
(1)求角C的大小;
(2)若c=2
| 3 |
| 3 |
考点:正弦定理,平面向量数量积的运算
专题:解三角形
分析:(1)根据向量共线建立条件关系,利用三角函数的关系式,即可求角C的大小;
(2)根据三角形的面积公式,以及余弦定理建立方程组,即可得到结论.
(2)根据三角形的面积公式,以及余弦定理建立方程组,即可得到结论.
解答:
解:(1)∵向量
=(cosB,2cos2
-1)与向量
=(2a-b,c)共线,
∴ccosB=(2a-b)cosC,
根据正弦定理得sinCcosB=(2sinA-sinB)cosC,
∴sinCcosB+sinBcosC=2sinAcosC,
即sinA═2sinAcosC,
∴cosC=
,即C=
.
(2)∵c2=a2+b2-2abcosC,
∴a2+s2-ab=12,①
∵S△ABC=2
=
absinC,
∴ab=8,②,
由①②得
或
.
| m |
| C |
| 2 |
| n |
∴ccosB=(2a-b)cosC,
根据正弦定理得sinCcosB=(2sinA-sinB)cosC,
∴sinCcosB+sinBcosC=2sinAcosC,
即sinA═2sinAcosC,
∴cosC=
| 1 |
| 2 |
| π |
| 3 |
(2)∵c2=a2+b2-2abcosC,
∴a2+s2-ab=12,①
∵S△ABC=2
| 3 |
| 1 |
| 2 |
∴ab=8,②,
由①②得
|
|
点评:本题主要考查正弦定理和余弦定理的应用,要求熟练掌握相应的定理和公式.

练习册系列答案
相关题目
如果一个空间几何体的正视图、侧视图、俯视图都是直径等于6的圆,那么这个空间几何体的体积等于( )
| A、144π | B、36π |
| C、24π | D、18π |
设集合A={x|0<x≤3},B={x|x<-1,或x>2},则A∩B=( )
| A、(2,3] |
| B、(-∞,-1)∪(0,+∞) |
| C、(-1,3] |
| D、(-∞,0)∪(2,+∞) |
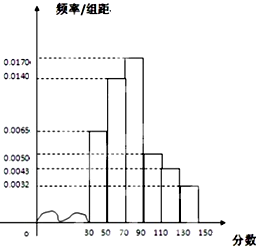 衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图:
衡水市为“市中学生知识竞赛”进行选拔性测试,且规定:成绩大于或等于90分的有参赛资格,90分以下(不包括90分)的则被淘汰.若现有500人参加测试,学生成绩的频率分布直方图如图: