题目内容

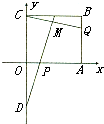如图所示，在直角坐标平面上的矩形OABC中，|OA|=2，|OC|=
3
，点P，Q满足
OP
=λ
OA
，
AQ
=1(1-λ)
AB
(λ∈R)，点D是C关于原点的对称点，直线DP与CQ相交于点M．
（1）求点M的轨迹方程；
（2）若过点F（-1，0）且斜率不为零的直线与点M的轨迹相交于G，H两点，直线AG和AH与定直线l：x=-4分别相交于点R，S，试判断以RS为直径的圆是否经过点F？说明理由．
考点：轨迹方程,直线与圆锥曲线的综合问题
专题：向量与圆锥曲线
分析：（1）设出动点M的坐标，由已知求出A、B、C、D的坐标，由已知的向量关系得到DP和CQ的直线方程，两式相乘消参后得到点M的轨迹方程；
（2）设出过点F（-1，0）且斜率不为0的直线CH的方程，和（1）中求出的曲线方程联立后利用根与系数关系得到G、H两点的纵坐标的和与积，把直线AG、AH的方程分别用G、H的坐标表示，求出R和S的坐标，代入数量积
FR
•
FS
，整理后再代入根与系数关系，化简后可得
FR
•
FS
=0，从而证得答案．
解答： 解：（1）设点M的坐标为（x，y），A（2，0），B（2，
3
），C（0，
3
），D（0，-
3
）．
由
OP
=λ
OA
，得点P坐标为（2λ，0），
由
AQ
=(1-λ)
AB
，得点Q的坐标为（2，
3
(1-λ)）．
于是，当λ≠0时，
直线DP的方程为：y+
3
=
3
2λ
x，①
直线CQ的方程为：y-
3
=
3
λ
-2
x．②
①×②得，y2-3=-
3
4
x2，即
x2
4
+
y2
3
=1．
当λ=0时，点M即为点C，而点C的坐标（0，
3
）也满足上式，
故点M的轨迹方程为
x2
4
+
y2
3
=1；
（2）设过点F（-1，0）且斜率不为0的直线CH的方程为x=my-1，且设G（x1，y1），H（x2，y2），
由
x=my-1
x2
4
+
y2
3
=1
，得（3m2+4）y2-6my-9=0    ③
由于方程③的判别式△=（-6m）2+36（3m2+4）＞0，
∴y1，y2是方程③的两根，且y1+y2=
6m
3m2+4
，y1y2=
-9
3m2+4
．
又A（2，0），
∴直线AG的方程为y=
y1
x1-2
(x-2)，因此点R的坐标为(-4，
-6y1
x1-2
)．
同理可得，直线AH的方程为y=
y2
x2-2
(x-2)，因此点S的坐标为(-4，
-6y2
x2-2
)．
∴
FR
•
FS
=(-3，
-6y1
x1-2
)•(-3，
-6y2
x2-2
)=9+
36y1y2
(x1-2)(x2-2)
．
又（x1-2）（x2-2）=（my1-3）（my2-3）=m2y1y2-3m（y1+y2）+9
=m2•
-9
3m2+4
-3m•
6m
3m2+4
+9=
36
3m2+4
．
于是
FR
•
FS
=9+
36y1y2
(x1-2)(x2-2)
=9+
36×(-9)
3m2+4
×
3m2+4
36
=0．
故点F在以RS为直径的圆周上．
点评：本题考查了轨迹方程的求法，是直线与圆锥曲线的综合题，涉及直线与圆锥曲线的关系问题，常把直线方程和圆锥曲线方程联立，利用根与系数的关系解题，是高考试卷中的压轴题．
练习册系列答案
相关题目
在实数集R中定义一种运算“*”，对任意a，b∈R，a*b为唯一确定的实数，且具有性质：
（1）对任意a∈R，a*0=a；
（2）对任意a，b，c∈R，（a*b）*c=（ab）*c+（a*c）+（b*c）-2c．
如：3*2=（3*2）*0=（3×2）*0+（3*0）+（2*0）-2×0=6+3+2-0=11．
关于函数f（x）=（2x）*
1
2x
的性质，有如下说法：
①函数f（x）的最小值为3；     
②函数f（x）的图象关于点（0，1）成中心对称；
③函数f（x）为奇函数；   
④函数f（x）的单调递增区间为(-∞，-
1
2
)，  &(
1
2
，+∞)．
其中所有正确说法的个数为（　　）
A、0B、1C、2D、3
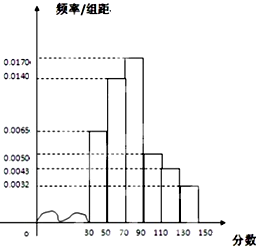衡水市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰．若现有500人参加测试，学生成绩的频率分布直方图如图：
（Ⅰ）求获得参赛资格的人数；
（Ⅱ）根据频率直方图，估算这500名学生测试的平均成绩；
（Ⅲ）若知识竞赛分初赛和复赛，在初赛中每人最多有5次选题答题的机会，累计答对3题或答错3题即终止，答对3题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为
1
9
，求甲在初赛中答题个数的分布列及数学期望．
已知函数f（x）=sinx+acosx的图象经过点（-
π
3
，0）．
（1）求实数a的值；
（2）设g（x）=[f（x）]2-2，求函数g（x）的最小正周期与单调递增区间．
甲、乙、丙、丁、戊5名学生进行劳动技术比赛，决出第一名至第五名的名次．比赛之后甲乙两位参赛者去询问成绩，回答者对甲说“根遗憾，你和乙都投有得到冠军”，对乙说“你当然不会是最差的”．
（Ⅰ）从上述回答分析，5人的名次排列可能有多少种不同的情况；
（Ⅱ）比赛组委会规定，第一名获奖金1000元，第二名获奖金800元，第三名获奖金600元，第四及第五名没有奖金，求丙获奖金数的期望．
已知函数f（x）=ex-1-x．
（Ⅰ）求f（x）的最小值；
（Ⅱ）当函数自变量的取值区间与对应函数值的取值区间相同时，这样的区间称为函数的保值区间．设g（x）=（f′（x）+1）（x2-1），试问函数g（x）在（1，+∞）上是否存在保值区间？若存在，请求出一个保值区间；若不存在，请说明理由．
已知x，y满足条件
x≥0
x-y+2≥0
2x+y-5≤0
，则z=x+3y+5的最大值是
 
．
对于定义域为[0，1]的函数f（x），如果同时满足以下三个条件：
①对任意的x∈[0，1]，总有f（x）≥0       
②f（1）=1
③若x1≥0，x2≥0，x1+x2≤1，都有f（x1+x2）≥f（x1）+f（x2） 成立；则称函数f（x）为?函数．下面有三个命题：
（1）若函数f（x）为?函数，则f（0）=0； 
（2）函数f（x）=2x-1（x∈[0，1]）是?函数；
（3）若函数f（x）是?函数，假定存在x0∈[0，1]，使得f（x0）∈[0，1]，且f[f（x0）]=x0，则f（x0）=x0；         
其中真命题是
 
．（填上所有真命题的序号）
设x∈R，若函数f（x）为单调递增函数，且对任意实数x，都有f[f（x）-ex]=e+1（e是自然对数的底数），则f（ln2）的值等于（　　）
A、1B、e+lC、3D、e+3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网