题目内容

O是△ABC外接圆的圆心，AB=1，AC=2，且
AO
=x
AB
+
4-x
8
AC
（x∈R，且x≠0），则△ABC的边长BC=
 
．
考点：平面向量数量积的运算,平面向量的基本定理及其意义
专题：解三角形,平面向量及应用
分析：画出图形，根据向量的数量积，求出∠BAC的余弦值，再利用余弦定理求出BC的值．
解答： 解：如图，；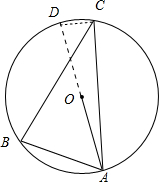
延长AO交圆O于点D，连接CD；
∴
AO
•
AC
=x
AB
•
AC
+
4-x
8
AC
2，
即
1
2
AD
•
AC
=x|
AB
|×|
AC
|cos∠BAC+
4-x
8
×22，
∴
1
2
（
AC
+
CD
）•
AC
=x×1×2cos∠BAC+
4-x
2
，
∴
1
2
×22+
1
2
×0=2xcos∠BAC+
4-x
2
，
∴x=4xcos∠BAC，
∴cos∠BAC=
1
4
；
又BC2=AB2+AC2-2AB•ACcos∠BAC
=12+22-2×1×2×
1
4

=4，
∴BC=2；
故答案为：2．
点评：本题考查了向量在几何中的应用以及余弦定理等知识，是综合题．
练习册系列答案
相关题目
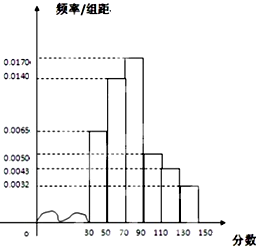衡水市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰．若现有500人参加测试，学生成绩的频率分布直方图如图：
（Ⅰ）求获得参赛资格的人数；
（Ⅱ）根据频率直方图，估算这500名学生测试的平均成绩；
（Ⅲ）若知识竞赛分初赛和复赛，在初赛中每人最多有5次选题答题的机会，累计答对3题或答错3题即终止，答对3题者方可参加复赛，已知参赛者甲答对每一个问题的概率都相同，并且相互之间没有影响，已知他连续两次答错的概率为
1
9
，求甲在初赛中答题个数的分布列及数学期望．
已知x，y满足条件
x≥0
x-y+2≥0
2x+y-5≤0
，则z=x+3y+5的最大值是
 
．
对于定义域为[0，1]的函数f（x），如果同时满足以下三个条件：
①对任意的x∈[0，1]，总有f（x）≥0       
②f（1）=1
③若x1≥0，x2≥0，x1+x2≤1，都有f（x1+x2）≥f（x1）+f（x2） 成立；则称函数f（x）为?函数．下面有三个命题：
（1）若函数f（x）为?函数，则f（0）=0； 
（2）函数f（x）=2x-1（x∈[0，1]）是?函数；
（3）若函数f（x）是?函数，假定存在x0∈[0，1]，使得f（x0）∈[0，1]，且f[f（x0）]=x0，则f（x0）=x0；         
其中真命题是
 
．（填上所有真命题的序号）
若在平面直角坐标系内过点P(1，
3
)且与原点的距离为d的直线有两条，则d的取值范围是
 
．
下列命题：
①?x∈R，x2+1＞0；
②?x∈N，x2≥1；
③?x∈Z，x3＜1；
④?x∈Q，x2=3； 
⑤?x∈R，x2-3x+2=0
⑥?x∈R，x2+1=0
其中所有真命题的序号是
 
．
已知变量x，y满足约束条件
x+y-5≤0
x-2y+1≤0
x-1≥0
，则z=x+2y的最大值是
 
．
设x∈R，若函数f（x）为单调递增函数，且对任意实数x，都有f[f（x）-ex]=e+1（e是自然对数的底数），则f（ln2）的值等于（　　）
A、1B、e+lC、3D、e+3
已知{an}是公差为d的等差数列，它的前n项和为Sn，S4=2S2+8．
（Ⅰ）求公差d的值；
（Ⅱ）若a1=1，设Tn是数列{
1
anan+1
}的前n项和，求使不等式Tn≥
1
18
(m2-5m)对所有的n∈N*恒成立的最大正整数m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网