题目内容
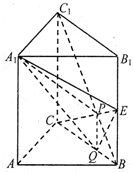如图在直三棱柱ABC-A1B1C1中，∠BAC=90°，AB=AA1=2，E是BB1的中点，且CE交BC1于点P，点Q在线段BC上，CQ=2QB．（1）证明：CC1∥平面A1PQ；
（2）若直线BC⊥平面A1PQ，求直线A1Q与平面BCC1B1所成角的余弦值．
考点：直线与平面所成的角,直线与平面平行的判定
专题：综合题,空间位置关系与距离,空间角
分析：（1）利用直三棱柱ABC-A1B1C1中，△BEP≌△C1CP，E是BB1的中点，可得PQ∥EB∥C1C，利用线面平行的判定定理，即可证明CC1∥平面A1PQ；
（2）延长QP与C1B相交于点H，连接A1H，A1Q，证明直线A1Q与平面BCC1B1所成角为∠A1QH，即可求得结论．
（2）延长QP与C1B相交于点H，连接A1H，A1Q，证明直线A1Q与平面BCC1B1所成角为∠A1QH，即可求得结论．
解答：
（1）证明：在直三棱柱ABC-A1B1C1中，△BEP≌△C1CP，E是BB1的中点，
∴
=
=
，
∴PQ∥EB∥C1C，
∵CC1?平面A1PQ，PQ?平面A1PQ，
∴CC1∥平面A1PQ；
（2）解：由（1）知，PQ∥C1C，
∴PQ∥AA1，
∴BC⊥平面A1PQA，
∴BC⊥AQ．
∵∠BAC=90°，CQ=2QB，
∴AC=2
，AQ-
．
延长QP与C1B相交于点H，连接A1H，A1Q，则
∵CC1⊥AQ，∴AQ⊥平面BCC1B1，
∵PQ∥AA1，HQ∥AA1，
∴四边形A1AHQ是平行四边形，
∴A1H∥AQ，
∴A1H⊥平面BCC1B1，
∴直线A1Q与平面BCC1B1所成角为∠A1QH，
∴cos∠A1QH=
=
=
．
∴
| CP |
| PE |
| 2 |
| 1 |
| CQ |
| BQ |
∴PQ∥EB∥C1C，
∵CC1?平面A1PQ，PQ?平面A1PQ，
∴CC1∥平面A1PQ；
（2）解：由（1）知，PQ∥C1C，
∴PQ∥AA1，
∴BC⊥平面A1PQA，
∴BC⊥AQ．
∵∠BAC=90°，CQ=2QB，
∴AC=2
| 2 |
2
| ||
| 3 |
延长QP与C1B相交于点H，连接A1H，A1Q，则
∵CC1⊥AQ，∴AQ⊥平面BCC1B1，
∵PQ∥AA1，HQ∥AA1，
∴四边形A1AHQ是平行四边形，
∴A1H∥AQ，
∴A1H⊥平面BCC1B1，
∴直线A1Q与平面BCC1B1所成角为∠A1QH，
∴cos∠A1QH=
| QH |
| A1Q |
| QH | ||
|
| ||
| 5 |
点评：本题考查线面平行，考查线面角，考查学生分析解决问题的能力，正确运用线面平行的判定定理是关键．
练习册系列答案
相关题目
已知实数x，y满足约束条件
，则w=
的最小值是（ ）
|
| y+1 |
| x |
| A、-2 | B、2 | C、-1 | D、1 |
设min{f(x)，g(x)}=
．若f（x）=x2+px+q的图象经过两点（α，0），（β，0），且存在整数n，使得n＜α＜β＜n+1成立，则（ ）
|
A、min{f(n)，f(n+1)}＞
| ||
B、min{f(n)，f(n+1)}＜
| ||
C、min{f(n)，f(n+1)}=
| ||
D、min{f(n)，f(n+1)}≥
|
设集合A={x|0＜x≤3}，B={x|x＜-1，或x＞2}，则A∩B=（ ）
| A、（2，3] |
| B、（-∞，-1）∪（0，+∞） |
| C、（-1，3] |
| D、（-∞，0）∪（2，+∞） |
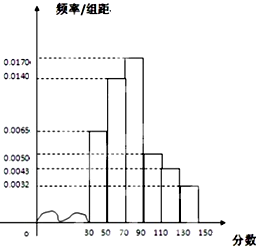衡水市为“市中学生知识竞赛”进行选拔性测试，且规定：成绩大于或等于90分的有参赛资格，90分以下（不包括90分）的则被淘汰．若现有500人参加测试，学生成绩的频率分布直方图如图：