题目内容
求函数y=
+
的值域.
| 1 |
| x2 |
| 1 |
| x |
考点:函数的值域
专题:计算题,函数的性质及应用
分析:由函数化简配方,从而求出值域.
解答:
解;∵y=
+
=(
+
)2-
,
∵(
+
)2≥0,
则(
+
)2-
≥-
,
则函数y=
+
的值域为[-
,+∞).
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
∵(
| 1 |
| x |
| 1 |
| 2 |
则(
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
则函数y=
| 1 |
| x2 |
| 1 |
| x |
| 1 |
| 4 |
点评:本题考查了函数值域的求法.高中函数值域求法有:1、观察法,2、配方法,3、反函数法,4、判别式法;5、换元法,6、数形结合法,7、不等式法,8、分离常数法,9、单调性法,10、利用导数求函数的值域,11、最值法,12、构造法,13、比例法.要根据题意选择.

练习册系列答案
相关题目
若f(x)=cosx在[-b,-a]上是增函数,则f(x)在[a,b]上是( )
| A、奇函数 | B、偶函数 |
| C、减函数 | D、增函数 |
已知圆C的方程为x2+y2-2x-3=0,直线l经过点(2,
)和圆C的圆心,则直线l的倾斜角等于( )
| 3 |
| A、30° | B、60° |
| C、120° | D、150° |
已知cosα=-
,且π<α<
,则tanα=( )
| 5 |
| 13 |
| 3π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
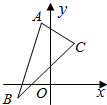 已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).
已知△ABC三个顶点是A(-1,4),B(-2,-1),C(2,3).