题目内容
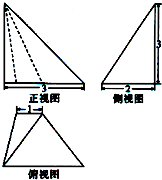
已知某个几何体的三视图如图所示,根据图中标出的尺寸(单位:cm),可得几何体的体积是( )cm3.

| A、4 | B、3 | C、6 | D、5 |
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:三视图复原的几何体是底面为直角梯形,一条侧棱垂直直角梯形的直角顶点的四棱锥,结合三视图的数据,求出几何体的体积.
解答:
解:三视图复原的几何体是底面为直角梯形,
一条侧棱垂直直角梯形的直角顶点的四棱锥,
所以几何体的体积为:
×
×2×3=4
故选:A.

一条侧棱垂直直角梯形的直角顶点的四棱锥,
所以几何体的体积为:
| 1 |
| 3 |
| 1+3 |
| 2 |
故选:A.
点评:本题是基础题,考查几何体的三视图,几何体的表面积的求法,准确判断几何体的形状是解题的关键.

练习册系列答案
相关题目
已知偶函数y=f(x)在区间[0,+∞)为增函数,则f(-3)和f(π)大小关系是( )
| A、f(-3)>f(π) |
| B、f(-3)<f(π) |
| C、f(-3)=f(π) |
| D、不能确定 |
设f(x-2)=2x,则f(3)的值为( )
| A、64 | B、8 | C、16 | D、32 |
已知函数f(x)=ax2-4ax+c,(a<0),当f(m)≥f(0)时,实数m满足的取值范围是( )
| A、(-∞,0]∪[4,+∞) |
| B、[0,4] |
| C、(0,4) |
| D、(0,+∞) |
如果命题“p且q”是假命题,“非p”是真命题,那么( )
| A、命题p一定是真命题 |
| B、命题q一定是真命题 |
| C、命题q一定是假命题 |
| D、命题q可以是真命题也可以是假命题 |