题目内容
已知椭圆
+
=1(a>b>0)的四个顶点顺次连接构成一个菱形,该菱形的面积为2
,又椭圆的离心率为
,则椭圆的标准方程是 .
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| ||
| 5 |
考点:椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:由离心率
求得a和c的关系,进而根据c2=a2-b2求得a和b的关系,进而根据
×2a×2b=2
求得a和b,则椭圆的方程可得.
| ||
| 5 |
| 1 |
| 2 |
| 10 |
解答:
解:由e=
=
,得3a2=5c2.
再由c2=a2-b2,解得a=
b.
由题意可知
×2a×2b=2
,即ab=
.
解方程得a=
,b2=
.
所以椭圆的方程为
+
=1.
故答案为:
+
=1
| c |
| a |
| ||
| 5 |
再由c2=a2-b2,解得a=
5
| ||
| 2 |
由题意可知
| 1 |
| 2 |
| 10 |
| 10 |
解方程得a=
| 10 |
| 2 | ||
|
所以椭圆的方程为
| x2 |
| 10 |
| ||
| 2 |
故答案为:
| x2 |
| 10 |
| ||
| 2 |
点评:本小题主要考查椭圆的标准方程和几何性质、考查计算能力.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
设M=
,N=
,P=
,Q
,则M与N、P与Q的大小关系为( )
| 102012+1 |
| 102013+1 |
| 102013+1 |
| 102014+1 |
| 102012+9 |
| 102013+100 |
| 102013+9 |
| 102014+100 |
| A、M>N,P<Q |
| B、M>N,P<Q |
| C、M>N,P<Q |
| D、M>N,P<Q |
已知偶函数y=f(x)在区间[0,+∞)为增函数,则f(-3)和f(π)大小关系是( )
| A、f(-3)>f(π) |
| B、f(-3)<f(π) |
| C、f(-3)=f(π) |
| D、不能确定 |
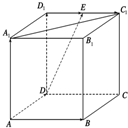 如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.
如图所示,在正方体ABCD-A1B1C1D1中,E为D1C1的中点,N为BC的中点.