题目内容
写出下列数列的一个通项公式:
(1)
,
,
,
,…;
(2)1,2,4,8,…;
(3)
,
,
,
,….
(1)
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
(2)1,2,4,8,…;
(3)
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 11 |
| 2 |
| 7 |
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:根据题意,观察每一个数列的各项特征,根据特征写出对应的通项公式.
解答:
解:(1)
,
,
,
,…;
观察该数列的每一项的特征是
,
,
,
,…;
∴an=
,n∈N*;
(2)1,2,4,8,…;
观察该数列的每一项的特征是
20,21,22,23,…;
∴an=2n-1,n∈N*;
(3)
,
,
,
,…;
观察该数列的每一项的特征是
,
,
,
,…;
∴an=
,n∈N*.
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
观察该数列的每一项的特征是
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 4×5 |
∴an=
| 1 |
| n(n+1) |
(2)1,2,4,8,…;
观察该数列的每一项的特征是
20,21,22,23,…;
∴an=2n-1,n∈N*;
(3)
| 4 |
| 5 |
| 1 |
| 2 |
| 4 |
| 11 |
| 2 |
| 7 |
观察该数列的每一项的特征是
| 4 |
| 5 |
| 4 |
| 8 |
| 4 |
| 11 |
| 4 |
| 14 |
∴an=
| 4 |
| 3n+2 |
点评:本题考查了根据数列的前几项的特征,归纳猜想数列的通项公式的问题,是基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
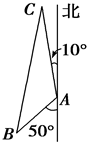 我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.
我舰在岛A南偏西50°相距12海里的B处发现敌舰正从岛A沿北偏西10°的方向以每小时10海里的速度航行,若我舰要用2小时追上敌舰,求我舰航行速度.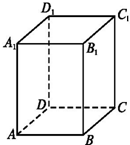 如图,已知长方体ABCD-A1B1C1D1中,AB=
如图,已知长方体ABCD-A1B1C1D1中,AB=