题目内容
已知f(t)=log2t,t∈[
,8],对于f(t)值域内的所有实数m,不等式x2+mx+4>2m+4x恒成立,求x的取值范围.
| 2 |
考点:对数的运算性质
专题:函数的性质及应用
分析:由t∈[
,8],得f(t)∈[
,3],x≠2.令g(m)=m(x-2)+(x-2)2,m∈[
,3],问题转化为g(m)在m∈[
,3]上恒对于0,由此能求出x的取值范围.
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵t∈[
,8],∴f(t)∈[
,3]
原题转化为:m(x-2)+(x-2)2>0恒成立,为m的一次函数(这里思维的转化很重要)
当x=2时,不等式不成立.
∴x≠2.令g(m)=m(x-2)+(x-2)2,m∈[
,3]
问题转化为g(m)在m∈[
,3]上恒大于0,
则:
,
解得:x>2或x<-1.
| 2 |
| 1 |
| 2 |
原题转化为:m(x-2)+(x-2)2>0恒成立,为m的一次函数(这里思维的转化很重要)
当x=2时,不等式不成立.
∴x≠2.令g(m)=m(x-2)+(x-2)2,m∈[
| 1 |
| 2 |
问题转化为g(m)在m∈[
| 1 |
| 2 |
则:
|
解得:x>2或x<-1.
点评:本题考查x的取值范围的求法,是中档题,解题时要注意对数性质的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
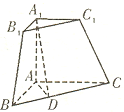 三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,直线A1A⊥平面ABC,A1A=
三棱锥被平行于底面ABC的平面所截得的几何体如图所示,截面为A1B1C1,直线A1A⊥平面ABC,A1A=