题目内容
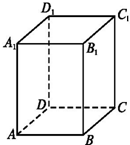如图，已知长方体ABCD-A1B1C1D1中，AB=| 3 |
| 3 |
（1）AD与A1C1所成的角是多少度？
（2）DD1与B1C所成的角是多少度？
考点：异面直线及其所成的角
专题：空间角
分析：（1）由A1C1∥AC，知AD与A1C1所成的角是∠DAC．
（2）由DD1∥CC1，知DD1与B1C所成的角是∠B1CC1．
（2）由DD1∥CC1，知DD1与B1C所成的角是∠B1CC1．
解答：
解：（1）∵A1C1∥AC，
∴AD与A1C1所成的角是∠DAC，
∵长方体ABCD-A1B1C1D1中，AB=
，AD=
，
∴∠DAC=45°，
∴AD与A1C1所成的角是45°．
（2）∵DD1∥CC1，
∴DD1与B1C所成的角是∠B1CC1，
∵长方体ABCD-A1B1C1D1中，AB=
，AD=
，AA1=1，
∴tan∠B1CC1=
=
，
∴∠B1CC1=60°，
∴DD1与B1C所成的角是60°．
∴AD与A1C1所成的角是∠DAC，
∵长方体ABCD-A1B1C1D1中，AB=
| 3 |
| 3 |
∴∠DAC=45°，
∴AD与A1C1所成的角是45°．
（2）∵DD1∥CC1，
∴DD1与B1C所成的角是∠B1CC1，
∵长方体ABCD-A1B1C1D1中，AB=
| 3 |
| 3 |
∴tan∠B1CC1=
| B1C1 |
| CC1 |
| 3 |
∴∠B1CC1=60°，
∴DD1与B1C所成的角是60°．
点评：本题考查异面直线所成角的求法，是基础题，解题时要认真审题．
练习册系列答案
相关题目
