题目内容
2.下列函数中,以$\frac{π}{2}$为最小正周期的奇函数是( )| A. | y=sin2x+cos2x | B. | y=sin(4x+$\frac{π}{2}$) | C. | y=sin2xcos2x | D. | y=sin22x-cos22x |
分析 由条件利用两角和差的三角公式,二倍角公式,诱导公式化简所给的函数的解析式,再利用三角函数的周期性和奇偶性,得出结论.
解答 解:∵y=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$)是非奇非偶函数,故排除A;
∵y=sin(4x+$\frac{π}{2}$)=cos4x为偶函数,故排除B;
∵y=sin2xcos2x=$\frac{1}{2}$sin4x是奇函数,周期为$\frac{2π}{4}$=$\frac{π}{2}$,故满足条件.
∵y=sin22x-cos22x=-cos4x,为偶函数,故排除D,
故选:C.
点评 本题主要考查两角和差的三角公式,二倍角公式,诱导公式的应用,三角函数的周期性和奇偶性,属于基础题.

练习册系列答案
相关题目
12.如果实数x,y满足条件$\left\{\begin{array}{l}{x-y-2≥0}\\{x-2≤0}\\{y+1≥0}\end{array}\right.$,则z=x+3y的最小值为-2.
10.已知圆C:(x-1)2+(y-2)2=2与y轴在第二象限所围区域的面积为S,直线y=2x+b分圆C的内部为两部分,其中一部分的面积也为S,则b=( )
| A. | $-\sqrt{6}$ | B. | ±$\sqrt{6}$ | C. | $-\sqrt{5}$ | D. | ±$\sqrt{5}$ |
7.已知A(2,0),B(-2,0),P(x,y),下列命题正确的是( )
| A. | 若P到A,B距离之和为4,则点P的轨迹为椭圆 | |
| B. | 若P到A,B距离之差为3,则点P的轨迹为双曲线 | |
| C. | 椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1上任意一点M(长轴端点除外)与A,B连线斜率之积是-$\frac{3}{4}$ | |
| D. | 双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{3}$=1上任意一点M(实轴端点除外)与A,B连线斜率之积是-$\frac{3}{4}$ |
14.在△ABC中,角A,B,C所对边分别为a,b,c,且(2b-a)•cosC=ccosA,c=3,sinA+sinB=2$\sqrt{6}$sinAsinB,则△ABC的面积为( )
| A. | $\frac{3\sqrt{3}}{8}$ | B. | 2 | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3\sqrt{3}}{4}$ |
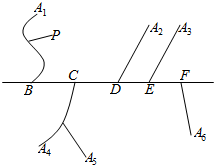 如图,一条公路的两侧有六个村庄,要建一个车站,要求到六个村庄的路程之和最小,应该选在哪里最合适?如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,那么这时车站设在什么地方好?
如图,一条公路的两侧有六个村庄,要建一个车站,要求到六个村庄的路程之和最小,应该选在哪里最合适?如果在P的地方增加一个村庄,并且沿地图的虚线修了一条小路,那么这时车站设在什么地方好?