题目内容
设数列{an}是等差数列,数列{bn}的前n项和Sn满足Sn=1-bn,(n∈N+),且a2-1=
,a5=
+1.
(Ⅰ)求数列{an}和{bn}的通项公式:
(Ⅱ)设Tn为数列{an.bn}的前n项和,求Tn.
| 1 |
| b1 |
| 1 |
| b3 |
(Ⅰ)求数列{an}和{bn}的通项公式:
(Ⅱ)设Tn为数列{an.bn}的前n项和,求Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)根据等差数列的通项公式,建立方程组,求出首项和公差,即可求数列{an}和{bn}的通项公式:
(Ⅱ)利用错位相减法即可求数列{an.bn}的前n项和.
(Ⅱ)利用错位相减法即可求数列{an.bn}的前n项和.
解答:
解(Ⅰ)由Sn=1-bn (1)
知当n=1时,b1=1-b1,∴b1=
.
当n≥2时,Sn-1=1-bn-1,(2)
(1)-(2)得2bn=bn-1,
∴
=
(n≥2),
∴{bn}是以
为首项以
为公比的等比数列,
∴bn=
,
∴b3=
,
∴a2=3,a5=9,∴3d=a5-a2=6,∴d=2.
故a1=1,an=1+2(n-1)=2n-1.
(Ⅱ)∵an.bn=
,
∴Sn=
+
+…+
①,
Sn=
+
+…+
+
②
①-②得
Sn=
+2(
+
+…+
)-
=
-
,
∴Sn=3-
.
知当n=1时,b1=1-b1,∴b1=
| 1 |
| 2 |
当n≥2时,Sn-1=1-bn-1,(2)
(1)-(2)得2bn=bn-1,
∴
| bn |
| bn-1 |
| 1 |
| 2 |
∴{bn}是以
| 1 |
| 2 |
| 1 |
| 2 |
∴bn=
| 1 |
| 2n |
∴b3=
| 1 |
| 8 |
∴a2=3,a5=9,∴3d=a5-a2=6,∴d=2.
故a1=1,an=1+2(n-1)=2n-1.
(Ⅱ)∵an.bn=
| 2n-1 |
| 2n |
∴Sn=
| 1 |
| 2 |
| 3 |
| 22 |
| 2n-1 |
| 2n |
| 1 |
| 2 |
| 1 |
| 22 |
| 3 |
| 23 |
| 2n-3 |
| 2n |
| 2n-1 |
| 2n+1 |
①-②得
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 23 |
| 1 |
| 2n |
| 2n-1 |
| 2n+1 |
| 3 |
| 2 |
| 2n+3 |
| 2n+1 |
∴Sn=3-
| 2n+3 |
| 2n |
点评:本题主要考查数列的通项公式以及数列求和,利用错误相减法是解决本题的关键,考查学生的计算能力.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
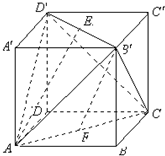 正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求:
正方体ABCD-A′B′C′D′的棱长等于2,E,F分别是B′D′,AC的中点.求: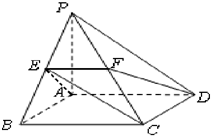 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,AB=AP=2,AD=4,E、F依次是PB、PC的中点. 如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,
如图所示,四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,