题目内容
已知函数f(x)=4x3+3tx2-6t2x+t-1(x∈R),其中t∈R.
(Ⅰ)当t=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)当t≠0时,求f(x)的单调区间;
(Ⅲ)若函数f(x)在区间(0,1)内存在零点,求实数t的取值范围.
(Ⅰ)当t=1时,求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)当t≠0时,求f(x)的单调区间;
(Ⅲ)若函数f(x)在区间(0,1)内存在零点,求实数t的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:综合题,导数的综合应用
分析:(Ⅰ)当t=1时,f(x)=4x3+3x2-6x,f′(x)=12x2+6x-6,由此能求出曲线y=f(x)在点(0,f(0))处的切线方程.
(Ⅱ)f′(x)=12x2+6tx-6t2,令f′(x)=0,解得x=-t,或x=
.由此进行分类讨论,能求出f(x)的单调区间.
(Ⅲ)当t>2时,
>1,f(x)在(0,1)内单调递减,f(0)=t-1>0,f(1)=-6t2+4t+3≤-6×4+4×2+3<0,即可得出结论.
(Ⅱ)f′(x)=12x2+6tx-6t2,令f′(x)=0,解得x=-t,或x=
| t |
| 2 |
(Ⅲ)当t>2时,
| t |
| 2 |
解答:
解:(Ⅰ)当t=1时,f(x)=4x3+3x2-6x,f(0)=0,f'(x)=12x2+6x-6f'(0)=-6.
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=-6x.-------4分
(Ⅱ)f'(x)=12x2+6tx-6t2,令f'(x)=0,解得x=-t,或x=
.
因为t≠0,以下分两种情况讨论:
(1)若t<0,则
<-t,当x变化时,f'(x),f(x)的变化情况如下表:
所以,f(x)的单调递增区间是(-∞,
),(-t,+∞);f(x)的单调递减区间是(
,-t).
(2)若t>0,则-t<
,当x变化时,f'(x),f(x)的变化情况如下表:
所以,f(x)的单调递增区间是(-∞,-t),(
,+∞);f(x)的单调递减区间是(-t,
).--------10分
(Ⅲ)由(Ⅱ)可知,当t>0时,f(x)在(0,
)内的单调递减,在(
,+∞)内单调递增,
当t>2时,
>1,f(x)在(0,1)内单调递减,f(0)=t-1>0,f(1)=-6t2+4t+3≤-6×4+4×2+3<0.
所以对任意t>2,在区间(0,1)内存在唯一的一个零点.-------------14分.
所以曲线y=f(x)在点(0,f(0))处的切线方程为y=-6x.-------4分
(Ⅱ)f'(x)=12x2+6tx-6t2,令f'(x)=0,解得x=-t,或x=
| t |
| 2 |
因为t≠0,以下分两种情况讨论:
(1)若t<0,则
| t |
| 2 |
| x | (-∞,
|
(
|
(-t,+∞) | ||||
| f'(x) | + | - | + | ||||
| f(x) |
| t |
| 2 |
| t |
| 2 |
(2)若t>0,则-t<
| t |
| 2 |
| x | (-∞,t) | (-t,
|
(
| ||||
| f'(x) | + | - | + | ||||
| f(x) |
| t |
| 2 |
| t |
| 2 |
(Ⅲ)由(Ⅱ)可知,当t>0时,f(x)在(0,
| t |
| 2 |
| t |
| 2 |
当t>2时,
| t |
| 2 |
所以对任意t>2,在区间(0,1)内存在唯一的一个零点.-------------14分.
点评:本题主要考查了导数的几何意义,利用导数研究函数的单调性、曲线的切线方程、函数零点、解不等式等基础知识,考查了计算能力和分类讨论的思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=
如图,四棱锥A-BCDE中,底面BCDE为矩形,侧面ABC⊥底面BCDE,BC=2,CD=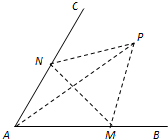 如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N (异于村庄A),要求PM=PN=MN=2(单位:千米).设∠AMN=θ.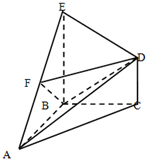 如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=2,CD=1,点F是AE的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题:
如图,在几何体ABCDE中,BE⊥平面ABC,CD∥BE,△ABC是等腰直角三角形,∠ABC=90°,且BE=AB=2,CD=1,点F是AE的中点.建立适当的空间直角坐标系,利用空间向量方法解答以下问题: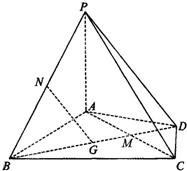 在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且
在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥AB,△ABC是正三角形,AC与BD的交点M恰好是AC中点,N为线段PB的中点,G在线段BM上,且