题目内容
在直角坐标系xOy中，已知过点P（-1，0）且倾斜角为
的直线l，以原点为极点，x轴的正半轴为极轴建立极坐标系，圆心C（3，
），半径r=1．
（Ⅰ）求直线l的参数方程及圆C的极坐标方程；
（Ⅱ）若直线l与圆C交于A，B两点，求AB的中点与点P的距离．
| π |
| 6 |
| π |
| 6 |
（Ⅰ）求直线l的参数方程及圆C的极坐标方程；
（Ⅱ）若直线l与圆C交于A，B两点，求AB的中点与点P的距离．
考点：参数方程化成普通方程
专题：坐标系和参数方程
分析：（Ⅰ）直接利用直线l的参数方程求出参数方程，利用圆的极坐标方程求出圆C的极坐标方程；
（Ⅱ）把参数方程代入圆的普通方程，求出参数，利用参数的几何意义，即可得到直线l与圆C交于A，B两点，AB的中点与点P的距离．
（Ⅱ）把参数方程代入圆的普通方程，求出参数，利用参数的几何意义，即可得到直线l与圆C交于A，B两点，AB的中点与点P的距离．
解答：
解：（Ⅰ）由已知得直线l的参数方程为
(t为参数)
圆心C(3cos
，3sin
)，半径1，
圆的方程为(x-
)2+(y-
)2=1
即x2+y2-3
x-3y+8=0
所以极坐标方程为ρ2-3
ρcosθ-3ρsinθ+8=0（6分）
（Ⅱ）把直线方程代入圆方程得t2-(
+6)t+9+3
=0，△=3＞0
设t1，t2是方程两根∴t1+t2=
+6
所以|PC|=|
|=
+3（12分）
|
圆心C(3cos
| π |
| 6 |
| π |
| 6 |
圆的方程为(x-
3
| ||
| 2 |
| 3 |
| 2 |
即x2+y2-3
| 3 |
所以极坐标方程为ρ2-3
| 3 |
（Ⅱ）把直线方程代入圆方程得t2-(
| 3 |
| 3 |
设t1，t2是方程两根∴t1+t2=
| 3 |
所以|PC|=|
| t1+t2 |
| 2 |
| ||
| 2 |
点评：本题考查参数方程的求法，参数的几何意义的应用，考查计算能力．
练习册系列答案
相关题目
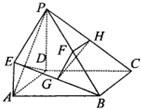如图所示，ABCD是边长为2的正方形，PD⊥平面ABCD，AD=PD=2EA，F，G，H分别为PB，EB，PC的中点．
在Rt△AOB中，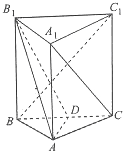
在三棱柱ABC-A1B1C1中，已知平面BB1C1C⊥平面ABC，AB=AC，D是BC中点，且B1D⊥BC1．