题目内容
由y=ex,x=0,y=2所围成的曲边梯形的面积为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:定积分的简单应用
专题:导数的综合应用
分析:画出图形,利用定积分的定义求解即可.
解答:
 解:由y=ex,x=0,y=2所围成的曲边梯形如图:y=ex,可得x=lny,
解:由y=ex,x=0,y=2所围成的曲边梯形如图:y=ex,可得x=lny,
曲边梯形的面积转化为对y的积分,即
lnydy.
故选:A.
 解:由y=ex,x=0,y=2所围成的曲边梯形如图:y=ex,可得x=lny,
解:由y=ex,x=0,y=2所围成的曲边梯形如图:y=ex,可得x=lny,曲边梯形的面积转化为对y的积分,即
| ∫ | 2 1 |
故选:A.
点评:本题考查定积分的简单应用,基本知识的考查.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
若(x+
)4=a0+a1x+a2x2+a3x3+a4x4,则(a0+a2+a4)2-(a1+a3)2的值为( )
| 3 |
| A、-16 | ||
| B、16 | ||
C、
| ||
D、
|
设集合A={x|
<0},B={x|log2(x-1)<0},那么“x∈A”是“x∈B”的( )
| x-2 |
| x-1 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分又不必要条件 |
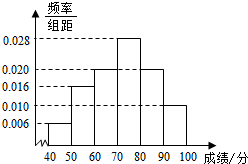 某校高三文科(1)班学生参加“江南十校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.
某校高三文科(1)班学生参加“江南十校”联考,其数学成绩(已折合成百分制)的频率分布直方图如图所示,其中成绩分布敬意为[40,50),[50,60),[60,70),[70,80),[80,90),[90,100],现已知成绩落在[90,100]的有5人.