题目内容
幂函数y=x m2+2m-3（m∈N）在区间（0，+∞）上是减函数，则m= ．
考点：幂函数的单调性、奇偶性及其应用,幂函数的概念、解析式、定义域、值域
专题：计算题,函数的性质及应用,不等式的解法及应用
分析：根据幂函数的性质，可得m2+2m-3＜0，解不等式求得自然数解，即可得到m=0．
解答：
解：由幂函数y=xm2+2m-3在（0，+∞）为减函数，
则m2+2m-3＜0，
解得-3＜m＜1．
由于m∈N，
则m=0．
故答案为：0．
则m2+2m-3＜0，
解得-3＜m＜1．
由于m∈N，
则m=0．
故答案为：0．
点评：本题考查幂函数的性质，主要考查二次不等式的解法，属于基础题．
练习册系列答案
课堂小作业系列答案
黄冈小状元口算速算练习册系列答案
成功训练计划系列答案
倍速训练法直通中考考点系列答案
一卷搞定系列答案
名校作业本系列答案
相关题目
执行如图所示的程序框图，若输入x=-1，则输入y的值为（ ）
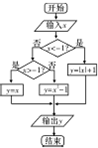
| A、-1 | B、0 | C、1 | D、2 |
由y=ex，x=0，y=2所围成的曲边梯形的面积为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若函数f（x）=sin（ωx-
）（ω＞0）在区间（0，
）上单调递增，则ω的取值范围是（ ）
| π |
| 4 |
| π |
| 2 |
A、（0，
| ||
B、[1，
| ||
| C、[1，2] | ||
| D、（0，2] |
设变量x，y满足约束条件
，则z=2x-2y的取值范围为（ ）
|
| A、[4，32] | ||
B、[
| ||
| C、[8，16] | ||
D、[
|