题目内容
已知函数f(x)=
+alnx,其中a为实常数.
(1)求f(x)的极值;
(2)若对任意x1,x2∈[1,3],且x1<x2,恒有
-
>|f(x1)-f(x2)|成立,求a的取值范围.
| 1 |
| x |
(1)求f(x)的极值;
(2)若对任意x1,x2∈[1,3],且x1<x2,恒有
| 1 |
| x1 |
| 1 |
| x2 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,导数的综合应用
分析:(1)f(x)的定义域为(0,+∞),求导f′(x)=
,由导数的正负确定函数的单调性及极值;
(2)|f(x1)-f(x2)|<
-
,?x1,x2∈[1,3],x1<x2恒成立可化为
对?x1,x2∈[1,3],x1<x2恒成立,从而可得g(x)=f(x)-
=alnx在[1,3]递增,h(x)=f(x)+
=
alnx+
在[1,3]递减;从而化为导数的正负问题.
| ax-1 |
| x2 |
(2)|f(x1)-f(x2)|<
| 1 |
| x1 |
| 1 |
| x2 |
|
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 2 |
| x |
解答:
解:(1)由已知f(x)的定义域为(0,+∞),
f′(x)=
,
当a>0时,f(x)在(0,
)上单调递减,在(
,+∞)上单调递增;
当x=
时,f(x)有极小值a-alna,无极大值;
当a≤0时,f(x)在(0,+∞)递减,f(x)无极值;
(2)∵|f(x1)-f(x2)|<
-
,?x1,x2∈[1,3],x1<x2恒成立,
∴
对?x1,x2∈[1,3],x1<x2恒成立;
即
对?x1,x2∈[1,3],x1<x2恒成立;
∴g(x)=f(x)-
=alnx在[1,3]递增,h(x)=f(x)+
=
alnx+
在[1,3]递减;
从而有
对x∈[1,3]恒成立;
∴0<a≤
.
f′(x)=
| ax-1 |
| x2 |
当a>0时,f(x)在(0,
| 1 |
| a |
| 1 |
| a |
当x=
| 1 |
| a |
当a≤0时,f(x)在(0,+∞)递减,f(x)无极值;
(2)∵|f(x1)-f(x2)|<
| 1 |
| x1 |
| 1 |
| x2 |
∴
|
即
|
∴g(x)=f(x)-
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 2 |
| x |
从而有
|
∴0<a≤
| 2 |
| 3 |
点评:本题考查了导数的综合应用及恒成立问题的转化与应用,属于难题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
已知f(
)=
,则f′(x)等于( )
| 1 |
| x |
| x |
| 1+x |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
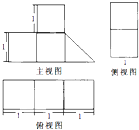
某几何体的三视图如图所示,则该几何体的体积为( )

A、
| ||
B、
| ||
C、
| ||
D、
|
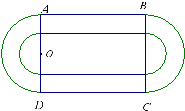 双峰一中是蔡和森的母校,已有百多年历史,学校教育教学质量稳步提高,今年高考喜获丰收,明年高考定会再创辉煌.为了贯彻全面发展的教育方针,学校决定新建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.
双峰一中是蔡和森的母校,已有百多年历史,学校教育教学质量稳步提高,今年高考喜获丰收,明年高考定会再创辉煌.为了贯彻全面发展的教育方针,学校决定新建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.已知塑胶跑道每平方米造价为150元,草皮每平方米造价为30元.