Question

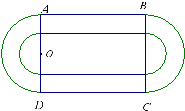双峰一中是蔡和森的母校，已有百多年历史，学校教育教学质量稳步提高，今年高考喜获丰收，明年高考定会再创辉煌．为了贯彻全面发展的教育方针，学校决定新建造一个面积为10000平方米的运动场．如图，运动场是由一个矩形ABCD和分别以AD、BC为直径的两个半圆组成．跑道是一条宽8米的塑胶跑道，运动场除跑道外，其他地方均铺设草皮．已知塑胶跑道每平方米造价为150元，草皮每平方米造价为30元．
（1）设半圆的半径OA=r（米），试建立塑胶跑道面积S与r的函数关系式S（r）；
（2）由于条件限制r∈[30，40]，问当r取何值时，运动场造价最低？最低造价是多少元？（精确到元，π≈3.1416）

Answer 1

考点：基本不等式在最值问题中的应用,函数模型的选择与应用

专题：应用题,函数的性质及应用

分析：（1）由面积公式写出S=π[r²-（r-8）²]+8×

10000-πr2

2r

×2，注明定义域；
（2）由函数的单调性求最值．

解答： 解：（1）塑胶跑道面积
S=π[r²-（r-8）²]+8×

10000-πr2

2r

×2
=

80000

r

+8πr-64π（0＜r＜

100

π

）；
（2）设运动场造价为y元；
y=150×（

80000

r

+8πr-64π）+30×（10000-

80000

r

-8πr+64π）
=300000+120（

80000

r

+8πr）-7680π；
∵r∈[30，40]；函数y是r的减函数，
∴当r=40时，运动场造价最低为626510元．

点评：本题考查了学生将实际问题转化为数学问题的能力，同时考查了函数的单调性的应用，属于中档题．