题目内容

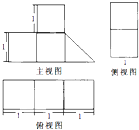
某几何体的三视图如图所示，则该几何体的体积为（　　）
A、
7
3
B、
9
2
C、
7
2
D、
9
4
考点：由三视图求面积、体积
专题：空间位置关系与距离
分析：先由三视图判断出几何体的形状及度量长度，然后利用棱锥的体积公式，可得答案．
解答： 解：由三视图得，该几何体为以主视图为底面的棱柱，
其底面面积S=
7
2
，
高h=1，
故棱柱的体积V=Sh=
7
2
，
故选：C
点评：解决三视图的题目，关键是由三视图判断出几何体的形状及度量长度，然后利用几何体的面积及体积公式解决．
练习册系列答案
相关题目
设递增数列{an}满足al=1，al、a2、a5成等比数列，且对任意n∈N*，函数．f（ x）=（an+2-an+1）x-（an-an-1）sinx+ancosx满足f′（π）=0．
（I）求数列{an}的通项公式；
（Ⅱ）若数列{an}的前n项和为Sn，bn=
1
Sn
，数列{bn}的前n项和为Tn，证明：Tn＜2．
过圆内一点的最长弦与最短弦所在直线方程分别为（a+1）x+（2a-1）y+a+8=0与ax-2y+4=0，则实数a=
 
．
已知函数f（x）=
1
x
+alnx，其中a为实常数．
（1）求f（x）的极值；
（2）若对任意x1，x2∈[1，3]，且x1＜x2，恒有
1
x1
-
1
x2
＞|f（x1）-f（x2）|成立，求a的取值范围．
已知A，B，C，D，E为抛物线y=
1
4
x2上不同的五个点，焦点为F，且
FA
+
FB
+
FC
+
FD
+
FE
=
0
，则|
FA
|+|
FB
|+|
FC
|+|
FD
|+|
FE
|=
 
．
已知图中（1）、（2）、（3）分别是一个立体模型的正视图、左视图、俯视图，这个立体模型由若干个棱长为1的小正方体组成，则这个立体模型的体积的所有可能值为
 
．
已知y=sinxcosx+sin2x可化为
 
：
①
2
2
sin（2x-
π
4
）+
1
2
；
②
2
2
sin（2x+
π
4
）-
1
2
；
③sin（2x-
π
4
）+
1
2
；
④2sin（2x+
3π
4
）+1．
设实数a，b均为区间[0，1]内的随机数，则关于x的不等式bx2+ax+
1
4
＜0有实数解的概率为（　　）
A、
1
2
B、
1
6
C、
1
3
D、
2
3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网