题目内容
已知sinα=m(|m|≤1),求tanα的值.
考点:同角三角函数基本关系的运用
专题:三角函数的求值
分析:利用平方关系求余弦,再利用商数关系求正切,注意讨论
解答:
解:当α∈(2kπ,2kπ+
),则cosα=
,tanα=
;(k∈Z)
当α∈(2kπ+
,2kπ+π),则tanα=-
;(k∈Z)
当α∈(2kπ+π,2kπ+
),则tanα=
;(k∈Z)
当α∈(2kπ+
,2kπ),则tanα=-
;(k∈Z)
| π |
| 2 |
| 1-m2 |
| |m| | ||
|
当α∈(2kπ+
| π |
| 2 |
| |m| | ||
|
当α∈(2kπ+π,2kπ+
| 3π |
| 2 |
| |m| | ||
|
当α∈(2kπ+
| 3π |
| 2 |
| |m| | ||
|
点评:本题主要考查同角三角函数关系,关键是分类讨论,避免漏解

练习册系列答案
相关题目
已知F是椭圆
+
=1(a>b>0)的右焦点,过点F作斜率为2的直线l使它与圆x2+y2=b2相切,则椭圆离心率是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
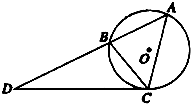 如图所示,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD=
如图所示,圆O是△ABC的外接圆,过点C的切线交AB的延长线于点D,CD= 如图,在四边形ABCD中,AB=2AD=1,AC=
如图,在四边形ABCD中,AB=2AD=1,AC=