题目内容

2．已知{an}为等差数列，若a1=6，a3+a5=0，则数列{an}的通项公式为an=8-2n．

分析 利用等差数列的通项公式即可得出．

解答 解：设等差数列{an}的公差为d，∵a1=6，a3+a5=0，
∴2×6+6d=0，解得d=-2．
∴an=6-2（n-1）=8-2n．
故答案为：an=8-2n．

点评 本题考查了等差数列的通项公式，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
12．已知二次函数f（x）=ax2-2x+c的值域为[0，+∞），则$\frac{9}{a}+\frac{1}{c}$的最小值为（　　）
A．3B．6C．9D．12
13．欧拉，瑞士数学家，18世纪数学界最杰出的人物之一，是有史以来最多遗产的数学家，数学史上称十八世纪为“欧拉时代”．1735年，他提出了欧拉公式：eiθ=cosθ+isinθ．被后人称为“最引人注目的数学公式”．若$θ=\frac{2π}{3}$，则复数z=eiθ对应复平面内的点所在的象限为（　　）
A．第一象限B．第二象限C．第三象限D．第四象限
10．函数y=1-2sin2（2x）的最小正周期是$\frac{π}{2}$．
17．设F1、F2分别为椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左、右焦点，点A为椭圆C的左顶点，点B为椭圆C的上顶点，且|AB|=$\sqrt{3}$，△BF1F2为直角三角形．
（1）求椭圆C的方程；
（2）设直线y=kx+2与椭圆交于P、Q两点，且OP⊥OQ，求实数k的值．
7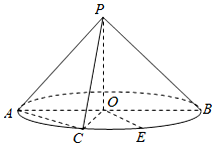．如图，圆锥的底面圆心为O，直径为AB，C为半圆弧AB的中点，E为劣弧CB的中点，且AB=2PO=2$\sqrt{2}$．
（1）求异面直线PC与OE所成的角的大小；
（2）求二面角P-AC-E的大小．
6．设函数f（x）=$\frac{2}{x}$-2+2alnx．
（1）讨论函数f（x）的单调性；
（2）若f（x）在区间[$\frac{1}{2}$，2]上的最小值为0，求实数a的值．
3．过正方体ABCD-A1B1C1D1的顶点A作平面α，使得正方体的各棱与平面α所成的角均相等，则满足条件的平面α的个数是（　　）
A．1B．4C．6D．8
4．已知等差数列{an}为各项均为正数，其前n项和为Sn，若a1=1，$\sqrt{{S}_{3}}$=a2，则a8=（　　）
A．12B．13C．14D．15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网