题目内容
15.甲、乙两家外卖公司,其单个送餐员的日工资方案如下:甲公司底薪70元,每单提成2元;乙公司无底薪,40单以内(含40 单)的部分每单提成4元,超出40 单的部分每单提成6元.假设同一公司的送餐员同一天的送餐单数相同,现从两家公司各抽取一名送餐员,分别记录其100天的送餐单数,得到如下频数分布表:甲公司被选取送餐员送餐单数频数分布表
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 20 | 40 | 20 | 10 | 10 |
| 送餐单数 | 38 | 39 | 40 | 41 | 42 |
| 天数 | 10 | 20 | 20 | 40 | 10 |
(1)若记乙公司单个送餐员日工资为X元,求X的分布列和数学期望;
(2)小明将要去其中一家公司应聘送餐员,若甲公司承诺根据每位送餐员的表现,每个季度将会增加300元至600元不等的奖金,如果每年按300个工作日计算,请利用所学的统计学知识为他作出选择,去哪一家公司的经济收入可能会多一些?
分析 (1)设乙公司送餐员送餐单数为a,写出X的所有可能取值,计算对应的概率,写出分布列和数学期望;
(2)求出甲公司送餐员日平均送餐单数,从而得到甲公司送餐员日平均工资,
再求出乙公司送餐员日平均工资,由此得出结论.
解答 解:(1)设乙公司送餐员送餐单数为a,
则当a=38时,X=38×4=152,
当a=39时,X=39×4=156,
当a=40时,X=40×4=160,
当a=41时,X=40×4+1×6=166,
当a=42时,X=40×4+2×6=172.
所以X的所有可能取值为152,156,160,166,172;
故X的分布列为:
| X | 152 | 156 | 160 | 166 | 172 |
| P | 0.1 | 0.2 | 0.2 | 0.4 | 0.1 |
(2)依题意,甲公司送餐员日平均送餐单数为
38×0.2+39×0.4+40×0.2+41×0.1+42×0.1=39.5,
所以甲公司送餐员日平均工资为70+2×39.5=149元;
由(1)得乙公司送餐员日平均工资为162元,
因为149<162,故推荐小明去乙公司应聘.
点评 本题主要考查了随机变量的分布列及数学期望的应用问题,是综合题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.欧拉,瑞士数学家,18世纪数学界最杰出的人物之一,是有史以来最多遗产的数学家,数学史上称十八世纪为“欧拉时代”.1735年,他提出了欧拉公式:eiθ=cosθ+isinθ.被后人称为“最引人注目的数学公式”.若$θ=\frac{2π}{3}$,则复数z=eiθ对应复平面内的点所在的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
10.$\frac{1-i}{1+i}$=( )
| A. | -i | B. | i | C. | 1 | D. | -1 |
7. 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
由表中的数据显示,x与y之间存在着线性相关关系,请将(2)的结果填入空白栏,并求出y关于x的回归直线方程.
 某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.
某公司为了解广告投入对销售收益的影响,在若干地区各投入4万元广告费用,并将各地的销售收益绘制成频率分布直方图(如图所示).由于工作人员操作失误,横轴的数据丢失,但可以确定横轴是从0开始计数的.[附:回归直线的斜率和截距的最小二乘估计公式分别为$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$.(1)根据频率分布直方图计算图中各小长方形的宽度;
(2)试估计该公司投入4万元广告费用之后,对应销售收益的平均值(以各组的区间中点值代表该组的取值);
(3)该公司按照类似的研究方法,测得另外一些数据,并整理得到下表:
| 广告投入x(单位:万元) | 1 | 2 | 3 | 4 | 5 |
| 销售收益y(单位:万元) | 2 | 3 | 2 | 7 |
4.已知等差数列{an}为各项均为正数,其前n项和为Sn,若a1=1,$\sqrt{{S}_{3}}$=a2,则a8=( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
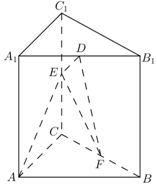 如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点.
如图,在直棱柱ABC-A1B1C1中,AA1=AB=AC=2,AB⊥AC,D,E,F分别是A1B1,CC1,BC的中点. 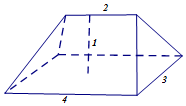 《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).
《九章算术》卷第五《商功》中,有问题“今有刍甍,下广三丈,袤四丈,上袤二丈,无广,高一丈.问积几何?”,意思是:“今有底面为矩形的屋脊状的楔体,下底面宽3丈,长4丈;上棱长2丈,无宽,高1丈(如图).