题目内容
3.已知函数f(x)=ex[x2-(a+2)x+b],曲线y=f(x)在x=0处的切线方程为2a2x+y-b=0,其中e是自然对数的底数).(Ⅰ)确定a,b的关系式(用a表示b);
(Ⅱ)对于任意负数a,总存在x>0,使f(x)<M成立,求实数M的取值范围.
分析 (Ⅰ)求导数,利用曲线y=f(x)在x=0处的切线方程为2a2x+y-b=0确定a,b的关系式(用a表示b);
(Ⅱ)对于任意负数a,总存在x>0,使f(x)<M成立,即对于任意负数a,x>0,使f(x)min<M成立,即可求实数M的取值范围.
解答 解:(Ⅰ)∵f(x)=ex[x2-(a+2)x+b],
∴f′(x)=ex[x2-ax+b-(a+2)],
∴f′(0)=-2a2,∴b=a+2-2a2;
(Ⅱ)对于任意负数a,总存在x>0,使f(x)<M成立,
即对于任意负数a,x>0,使f(x)min<M成立,
由(Ⅰ)可知f′(x)=ex(x-2a)(x+a),
令f′(x)=0,可得x=2a,或x=-a.
a<0,0<x<-a,f′(x)<0,函数单调递减,x>-a,f′(x)>0,函数单调递增,
∴x>0,f(x)min=f(-a)=e-a(3a+2),
令g(a)=e-a(3a+2),则g′(a)=e-a(1-3a)>0,此时函数单调递增,即g(a)<g(0)=2,
∴M≥2.
点评 本题考查函数的切线方程的求法,考查函数的单调性的求法.解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
14.已知函数$f(x)=\sqrt{3}sin2x-cos2x$的图象在区间$[{0,\frac{a}{3}}]$和$[{2a,\frac{4π}{3}}]$上均单调递增,则正数a的取值范围是( )
| A. | $[{\frac{π}{6},\frac{5π}{12}}]$ | B. | $[{\frac{5π}{12},π}]$ | C. | $[{\frac{π}{4},π}]$ | D. | $[{\frac{π}{4},\frac{2π}{3}}]$ |
11.已知集合M={x|1<x≤3},若N={x|2<x≤5},则M∪N=( )
| A. | {x|1<x≤5} | B. | {x|2<x≤3} | C. | {x|1≤x<2或3≤x≤5}} | D. | {x|1≤x≤5} |
18.已知实数x,y满足不等式组$\left\{\begin{array}{l}{-3≤3x-y≤-1}\\{-1≤x+y≤1}\end{array}\right.$,若z=ax+y有最大值$\frac{5}{2}$,则实数a的值是( )
| A. | 2 | B. | $\frac{5}{2}$ | C. | -2 | D. | -$\frac{5}{2}$ |
8. 执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
 执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )
执行右边的程序框图,若输入?=0.01,则输出的e精确到?的近似值为( )| A. | 2.69 | B. | 2.70 | C. | 2.71 | D. | 2.72 |
15.执行如图的程序框图,则输出的结果为( )
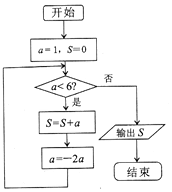

| A. | 15 | B. | 3 | C. | -11 | D. | -5 |
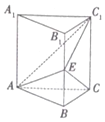 如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.
如图,在直三棱柱ABC-A1B1C1中,△ABC是正三角形,E是棱BB1的中点.