题目内容
1.已知向量$\overrightarrow a=(cosωx,sinωx)$,$\overrightarrow b=(cosωx,\sqrt{3}cosωx)$,其中ω>0,函数$f(x)=\overrightarrow a•\overrightarrow b-\frac{1}{2}$,其最小正周期为π.(1)求函数f(x)的表达式及单调减区间;
(2)在△ABC的内角A,B,C所对的边分别为a,b,c,S为其面积,若f($\frac{A}{2}$)=1,b=1,S△ABC=$\sqrt{3}$,求a的值.
分析 (1)利用两个向量的数量积公式,三角恒等变换化简函数的解析式,再利用正弦函数的周期性和单调性,得出结论.
(2)由f($\frac{A}{2}$)=1,求得A=$\frac{π}{3}$,根据S△ABC =$\sqrt{3}$,求得 c=4,再利用余弦定理求得a=$\sqrt{{b}^{2}{+c}^{2}-2bc•cosA}$ 的值.
解答 解:(1)函数$f(x)=\overrightarrow a•\overrightarrow b-\frac{1}{2}$=cos2ωx+$\sqrt{3}$sinωxcosωx-$\frac{1}{2}$
=$\frac{1}{2}$cos2ωx+$\frac{\sqrt{3}}{2}$sin2ωx=sin(2ωx+$\frac{π}{6}$),
其最小正周期为$\frac{2π}{2ω}$=π,∴ω=1,f(x)=sin(2x+$\frac{π}{6}$).
令2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,求得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,
故函数的减区间为[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
(2)在△ABC中,∵f($\frac{A}{2}$)=sin(A+$\frac{π}{6}$)=1,
∴A=$\frac{π}{3}$,又 b=1,S△ABC=$\frac{1}{2}$bc•sinA=$\frac{1}{2}$•1•c•$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴c=4,∴a=$\sqrt{{b}^{2}{+c}^{2}-2bc•cosA}$=$\sqrt{1+16-8•\frac{1}{2}}$=$\sqrt{13}$.
点评 本题主要考查两个向量的数量积公式,三角恒等变换,正弦函数的周期性和单调性,余弦定理的应用,属于中档题.

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案| A. | cosα | B. | -cosα | C. | sinα | D. | -sinα |
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | 2-$\sqrt{2}$ |
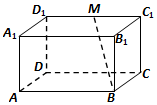 如图,在长方体ABCD-A1B1C1D1中,AB=2AD=4,A A1=2$\sqrt{2}$,M是C1D1的中点.
如图,在长方体ABCD-A1B1C1D1中,AB=2AD=4,A A1=2$\sqrt{2}$,M是C1D1的中点.