题目内容
11.在等比数列{an}中,an>0,公比q∈(0,1),且a1a5+2a3a5+a2a8=25,a3与a5的等比中项为2,求数列{an}的通项公式an=${({\frac{1}{2}})^{n-5}}$.分析 推导出a3,a5是方程x2-5x+4=0的两个根,且a3>a5.从而得到a3=4,a5=1,进而得到${a}_{1}=16,q=\frac{1}{2}$,由此能求出结果.
解答 解:∵在等比数列{an}中,an>0,公比q∈(0,1),
且a1a5+2a3a5+a2a8=25,a3与a5的等比中项为2,
∴$\left\{\begin{array}{l}{{a}_{3}+{a}_{5}=5}\\{{a}_{3}{a}_{5}=4}\end{array}\right.$,
∴a3,a5是方程x2-5x+4=0的两个根,且a3>a5.
解方程x2-5x+4=0,得a3=4,a5=1,
∴$\left\{\begin{array}{l}{{a}_{1}{q}^{2}=4}\\{{a}_{1}{q}^{4}=1}\end{array}\right.$,由q∈(0,1),解得${a}_{1}=16,q=\frac{1}{2}$,
∴${a}_{n}=16×(\frac{1}{2})^{n-1}$=($\frac{1}{2}$)n-5.
故答案为:an=${({\frac{1}{2}})^{n-5}}$.
点评 本题考查等差数列的通项公式的求法,是基础题,解题时要认真审题,注意利用等差数列的性质的合理运用.

练习册系列答案
相关题目
2.下列说法正确的是( )
| A. | 在频率分布直方图中,众数左边和右边的直方图的面积相等 | |
| B. | 为调查高三年级的240名学生完成作业所需的时间,由教务处对高三年级的学生进行编号,从001到240抽取学号最后一位为3的学生进行调查,则这种抽样方法为分层抽样 | |
| C. | “x≠1”是“x2-3x+2≠0”的充分不必要条件 | |
| D. | 命题p:“?x0∈R,${x_0}^2-3{x_0}+2<0$”的否定为:“?x∈R,x2-3x+2≥0” |
16.已知幂函数y=f(x)的图象过点(2,4),则log2f($\frac{1}{2}$)=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
20.设直线l与椭圆$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{8}=1$相交于A,B两点,与圆(x-1)2+y2=r2(r>0)相切于点M,且M为线段AB的中点,若这样的直线l恰有4条,则r的取值范围是( )
| A. | (1,$\sqrt{6}$) | B. | (2,$\sqrt{7}$) | C. | (2,$\sqrt{6}$) | D. | (1,$\sqrt{7}$) |
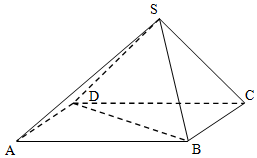 如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$.
如图所示,在四棱锥S-ABCD中,底面ABCD是矩形,侧面SDC⊥底面ABCD,且AB=2,SC=SD=$\sqrt{2}$. 已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.
已知F1,F2 分别是椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+y2=1,(a>1)的左、右焦点,P在椭圆上且到两个焦点F1,F2 的距离之和为2$\sqrt{2}$.