题目内容
6.在平面直角坐标系xOy中,不等式组$\left\{\begin{array}{l}{(x-y-1)(x+y-1)≥0}\\{-1≤x≤3}\end{array}\right.$表示的平面区域的面积为( )| A. | 4 | B. | 8 | C. | 12 | D. | 16 |
分析 画出约束条件的可行域,利用可行域求解三角形的面积即可.
解答 解:不等式组$\left\{\begin{array}{l}{(x-y-1)(x+y-1)≥0}\\{-1≤x≤3}\end{array}\right.$表示的平面区域如图:
阴影部分是两个全等的三角形,A(-1,2),B(-1,-2),E(1,0),
阴影部分的面积为:$2×\frac{1}{2}×4×2$=8.
故选:B.
点评 本题考查解得的线性规划的应用,考查数形结合以及计算能力.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
16.2016年初,受国际油价大幅上涨的拉动,一些石油替代型企业生产成本出现大幅度上升,近期,由于国际油价回落,石油替代型企业生产成本明显下降,某PVC行业企业的生产成本在8月份、9月份每月递增20%,国际油价回落之后,10月份、11月份的生产成本每月递减20%,那么该企业在11月底的生产成本与8月初比较( )
| A. | 不增不减 | B. | 约增加5% | C. | 约减少8% | D. | 约减少5% |
11.设定义在R上的函数f(x)的导函数为f′(x),且满足f(2-x)=f(x),$\frac{f′(x)}{x-1}$<0,若x1+x2>2,x1<x2,则( )
| A. | f(x1)<f(x2) | B. | f(x1)=f(x2) | ||
| C. | f(x1)>f(x2) | D. | f(x1)与f(x2)的大小不能确定 |
15.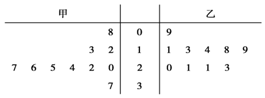 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
 某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )
某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.命中个数的茎叶图如图,则下面结论中错误的一个是( )| A. | 乙的众数是21 | B. | 甲的中位数是24 | ||
| C. | 甲的极差是29 | D. | 甲罚球命中率比乙高 |
16.已知幂函数y=f(x)的图象过点(2,4),则log2f($\frac{1}{2}$)=( )
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | 2 | D. | -2 |
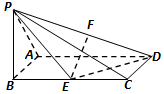 如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.
如图,已知PB⊥矩形ABCD所在的平面,E,F分别是BC,PD的中点,∠PAB=45°,AB=1,BC=2.