题目内容
18.已知函数f(x)是定义在R上的偶函数,且f(-x-1)=f(x-1),当x∈[-1,0]时,f(x)=-x3,则关于x的方程f(x)=|cosπx|在[-$\frac{5}{2}$,$\frac{1}{2}$]上的所有实数解之和为( )| A. | -7 | B. | -6 | C. | -3 | D. | -1 |
分析 由f(x)是偶函数说明函数图象关于y轴对称,由f(-x-1)=f(x-1),得到x=-1是函数的对称轴,画出函数f(x)的图象,只要找出函数f(x)的图象与y=|cosπx|在[-$\frac{5}{2}$,$\frac{1}{2}$]上内交点的情况,根据对称性即可求出答案.
解答 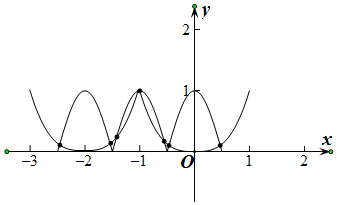 解:∵函数f(x)是定义在R上的偶函数,f(-x-1)=f(x-1),
解:∵函数f(x)是定义在R上的偶函数,f(-x-1)=f(x-1),
∴x=-1是函数的对称轴,
分别画出y=f(x)与y=|cosπx|在[-$\frac{5}{2}$,$\frac{1}{2}$]上图象,
交点依次为x1,x2,x3,x4,x5,x6,x7,
∴x1+x7=-2,x2+x6=-2,x3+x5=-2,x4=-1,
∴x1+x2+x3+x4+x5+x6+x7=-2×3-1=-7,
故选:A
点评 本题考查了函数与方程的综合应用以及函数图象的对称性与奇偶性等知识点,数形结合是解决本题的关键,属中档题

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案
相关题目
12.若f(x)=xsinx,则函数f(x)的导函数f′(x)等于( )
| A. | 1-sinx | B. | x-sinx | C. | sinx+xcosx | D. | cosx-xsinx |
9.函数y=-lg(x+1)的图象是( )
| A. |  | B. |  | C. |  | D. |  |
13.若椭圆$\frac{x^2}{5}+\frac{y^2}{m}=1$的离心率为$e=\frac{1}{2}$,则m的值为( )
| A. | $\frac{20}{3}$ | B. | $\frac{15}{4}$或$\frac{20}{3}$ | C. | $\frac{15}{4}$ | D. | $\frac{20}{4}$ |
7.设e是椭圆$\frac{x^2}{k}+\frac{y^2}{4}=1$的离心率,且$e∈({\frac{1}{2},1})$,则实数k的取值范围是( )
| A. | (0,3) | B. | $({3,\frac{16}{3}})$ | C. | (0,2) | D. | $({0,3})∪({\frac{16}{3},+∞})$ |
8.下列幂函数中过点(0,0),(1,1)的偶函数是( )
| A. | $y={x^{\frac{1}{2}}}$ | B. | y=x2 | C. | y=x-1 | D. | y=x3 |