题目内容
13.若椭圆$\frac{x^2}{5}+\frac{y^2}{m}=1$的离心率为$e=\frac{1}{2}$,则m的值为( )| A. | $\frac{20}{3}$ | B. | $\frac{15}{4}$或$\frac{20}{3}$ | C. | $\frac{15}{4}$ | D. | $\frac{20}{4}$ |
分析 当m>5时,a2=m,b2=5,c2=m-5,e2=$\frac{m-5}{m}=\frac{1}{4}$⇒m;
当0<m<5时,a2=5,b2=m,c2=5-m,e2=$\frac{5-m}{5}=\frac{1}{4}$⇒m;
解答 解:当m>5时,a2=m,b2=5,c2=m-5,e2=$\frac{m-5}{m}=\frac{1}{4}$⇒m=$\frac{20}{3}$;
当0<m<5时,a2=5,b2=m,c2=5-m,e2=$\frac{5-m}{5}=\frac{1}{4}$⇒m=$\frac{15}{4}$;
故选:B.
点评 本题考查了椭圆的离心率,及分类讨论思想,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.函数f(x)=ax3+6x2+(a-1)x-5有极值的充要条件是( )
| A. | a=-3或a=4 | B. | -3<a<4 | C. | a>4或a<-3 | D. | a∈R |
18.已知函数f(x)是定义在R上的偶函数,且f(-x-1)=f(x-1),当x∈[-1,0]时,f(x)=-x3,则关于x的方程f(x)=|cosπx|在[-$\frac{5}{2}$,$\frac{1}{2}$]上的所有实数解之和为( )
| A. | -7 | B. | -6 | C. | -3 | D. | -1 |
2.男婴为24人,女婴为8人;出生时间在白天的男婴为31人,女婴为26人.
(1)将下面的2×2列联表补充完整;
(2)能否在犯错误的概率不超过0.1的前提下认为婴儿性别与出生时间有关系?
参考公式:(1)K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d);
(2)独立性检验的临界值表:
(1)将下面的2×2列联表补充完整;
| 出生时间 性别 | 晚上 | 白天 | 合计 |
| 男婴 | |||
| 女婴 | |||
| 合计 |
参考公式:(1)K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d);
(2)独立性检验的临界值表:
| P(K2≥k0) | 0.10 | 0.05 | 0.010 |
| k0 | 2.706 | 3.841 | 6.635 |
 如图:空间四边形ABCD中,E,F,G,H分别是AB,AD,CD,CB上的点,且EF∥GH,求证:EF∥BD.
如图:空间四边形ABCD中,E,F,G,H分别是AB,AD,CD,CB上的点,且EF∥GH,求证:EF∥BD.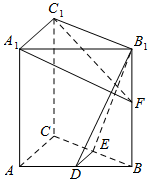 如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证:
如图,在直三棱柱ABC-A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B上,且B1D⊥A1F,A1C1⊥A1B1.求证: