题目内容
9.某同学从区间[-1,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…(xn,yn),该同学用随机模拟的方法估计n个数对中两数的平方和小于1(即落在以原点为圆心,1为半径的圆内)的个数,则满足上述条件的数对约有$\frac{nπ}{4}$个.分析 以面积为测度,建立方程,即可求出满足上述条件的数对.
解答  解:由题意,两数的平方和小于1,对应的区域的面积为$\frac{1}{4}$π•12,从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),对应的区域的面积为12,
解:由题意,两数的平方和小于1,对应的区域的面积为$\frac{1}{4}$π•12,从区间[0,1]随机抽取2n个数x1,x2,…,xn,y1,y2,…,yn,构成n个数对(x1,y1),(x2,y2),…,(xn,yn),对应的区域的面积为12,
∴$\frac{m}{n}=\frac{\frac{1}{4}π•{1}^{2}}{{1}^{2}}$,∴m=$\frac{nπ}{4}$.
故答案为$\frac{nπ}{4}$.
点评 古典概型和几何概型是我们学习的两大概型,古典概型要求能够列举出所有事件和发生事件的个数,而不能列举的就是几何概型,几何概型的概率的值是通过长度、面积和体积的比值得到.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
4.在10件同类产品中,有2次品,从中任取3件产品,其中不可能事件为( )
| A. | 3件都是正品 | B. | 至少有1件次品 | C. | 3件都是次品 | D. | 至少有1件正品 |
1.若0<x<1,则$\frac{1}{x}+\frac{2x}{1-x}$的最小值为( )
| A. | $2\sqrt{2}$ | B. | 1+$2\sqrt{2}$ | C. | 2+$2\sqrt{2}$ | D. | 3+$2\sqrt{2}$ |
16.已知集合P={x|1<3x≤9},Q={x∈Z|y=ln(-2x2+7x)},则P∩Q=( )
| A. | {1} | B. | {1,2} | C. | {2,3} | D. | {1,2,3} |
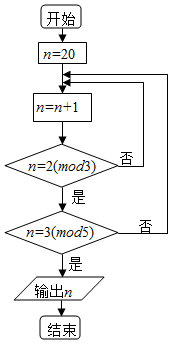 中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )
中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( )