题目内容
20.在△ABC中,BC=5,CA=8,∠C=60°,则$\overrightarrow{BC}•\overrightarrow{CA}$=-20.分析 由题意画出图形,直接代入数量积公式求解.
解答 解:如图,
∵BC=5,CA=8,∠C=60°,
∴$\overrightarrow{BC}•\overrightarrow{CA}$=$|\overrightarrow{BC}||\overrightarrow{CA}|cos120°=5×8×(-\frac{1}{2})=-20$.
故答案为:-20.
点评 本题考查平面向量的数量积运算,考查数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
11.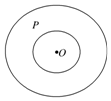 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )| A. | $\frac{1}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
15.化简 $\overrightarrow{AB}-\overrightarrow{CD}+\overrightarrow{BD}-\overrightarrow{AC}$的结果是( )
| A. | $\overrightarrow 0$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow{BD}$ | D. | $\overrightarrow{DA}$ |
5.已知△ABC的边长为a,b,c,定义它的等腰判别式为D=max{a-b,b-c,c-a}+min{a-b,b-c,c-a},则“D=0”是△ABC为等腰三角形的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.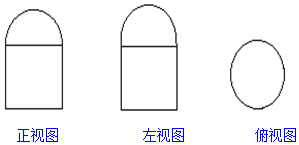 如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
 如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )| A. | 5π | B. | 6π | C. | 7π | D. | 8π |
 如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.
如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.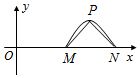 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象关于y轴对称,该函数的部分图象如图所示,△PMN是以MN为斜边的等腰直角三角形,且$|MN|•|MP|=2\sqrt{2}$,则f(1)的值为0.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象关于y轴对称,该函数的部分图象如图所示,△PMN是以MN为斜边的等腰直角三角形,且$|MN|•|MP|=2\sqrt{2}$,则f(1)的值为0.